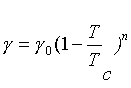
Pro vyjádření závislosti povrchového napětí na hustotě se užívá McLeodova rovnice [3]
| g=g0rn | (R2-5) |
n v této rovnici při odvozování z teoretického modelu pole ostatních částic s Lennardovým-Jonesovým potenciálem vychází 8/3 [4], pro polymery rovnice platí s hodnotou n 3 až 4,4, nejtypičtěji 4,0. Závislost povrchového napětí na hustotě poskytují i teorie, které jsou zmíněny v dalších kapitolách.
U čistých kapalin se stává povrchové napětí nenulovým při kritické teplotě, mezifázové napětí pak při kritické mísící teplotě. Pro teplotní závislost povrchového napětí navrhl van der Waals rovnici
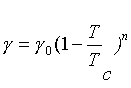 |
(36) |
kde n = 1,23; rovnice se s hodnotou n = 11/9 nazývá též Guggenheimovou. Hodnota γ0 se získá extrapolací povrchového napětí na nulovou teplotu.
Jak patrno, γ0 se získá extrapolací povrchového napětí na nulovou teplotu. Tato rovnice je použitelná i pro polymery. Z dalších rovnic pro povrchové napětí je možno uvést Eötvösovu rovnici
| dγ (VM)2/3/dT= k | (37) |
kde součin VM představuje objem připadající na jednu molekulu. Tato rovnice není vhodná pro polymery.
Další běžná rovnice je Ramsay - Shieldsova:
| γ.Vi2/3 = k(Tc - T - 6) | (38) |
kde V1 je objem jedné molekuly.
Teplotní součinitel povrchového napětí je derivací Guggenheimovy rovnice (36)
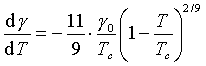 |
(39) |
Předpokládejme, že přichází v úvahu měření látky v rozsahu 300 - 600 K a že kritická teplota látky je 900 K. V takovém případě bude poměr teplotních součinitelů povrchového napětí při krajních teplotách uvedeného intervalu 22/9, tj. 1,17.
U polymerů bývá podmínka uvedené vzdálenosti od kritické teploty splněna podstatně výrazněji, tudíž lze u nich považovat teplotní závislost za lineární.
Platí-li McLeodova rovnice [3]
| g=g0rn | (40) |
a pokud teplotní závislost povrchového napětí připíšeme toliko změně hustoty, získáme pomocí této rovnice
| dg/dT=-nag | (41) |
kde a je součinitel teplotní roztažnosti.
V rovnici povrchového napětí odvozené pomocí Lennardova-Jonesova potenciálu [3] závisí na teplotě kromě hustoty ještě polární složka van der Waalsových sil, která s rostoucí teplotou slábne. To by mělo velikost teplotního součinitele o něco zvýšit.
Teplotní součinitel povrchového napětí se pohybuje v desetinách mN.m-1K-1, u polymerů kolem 5 - 10.10-2 mN.m-1K-1.
Již dřívější autoři [l4] dospěli k závěru, že veličina [P]:
[P] = V g1/4
je aditivní (V je zde molární objem) a lze její pomocí odhadovat povrchové napětí. Tato veličina byla nazvána parachor. Považujeme-li parachor za konstantu látky nezávislou na momentální hodnotě stavových veličin, je definiční rovnice parachoru konsistentní s McLeodovou rovnicí.
Podobně jako některé objemové vlastnosti q (skelná teplota, tepelná kapacita, teplotní objemová roztažnost, index lomu aj.) závisejí na molekulové hmotnosti
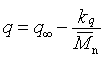
kde konstanta qµ odpovídá veličině q extrapolované na nekonečnou molekulovou hmotnost, lze očekávat u povrchových vlastností závislost
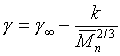 |
(R2-11) |
Vyjádřením hustoty pomocí molekulové hmotnosti [3], jejím dosazením do McLeodovy rovnice s exponentem n, rozvojem v mocninnou řadu podle M a zanedbáním vyšších členů získáme
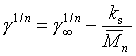 |
(R2-12) |
nebo
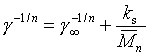
Tyto rovnice se užívají s hodnotou n = 4 a dávají někdy lepší výsledek než (r2-11) [l5], ale rozdíl v přesnosti není podstatný [3]. Hodnoty γµ v obou rovnicích jsou rozdílné. Závislost (r2-12) je však konzistentnější s experimentální závislostí g - T vysokomolekulárních látek i použitím parachoru.
V oblasti vysokých molekulových hmotností však shledávají Dee a Sauer [l6] výstižnější lineární závislost
γ=γµ-![]()
Doporučeny dále tyto články z textu doc. Lidmily Bartovské a doc. Marie Šiškové: