Spoluurčují hustotu a podstatně určují povrchové napětí, viskozitu, pevnost, pružnost a další mechanické vlastnosti.
Základní druhy mezimolekulárních sil (http://vydavatelstvi.vscht.cz/knihy/uid_es-001/hesla/mezimolekularni_interakce.html ) jsou:
Mezi dvěma plyny za normálních okolností nevzniká rozhraní.
Mezi kapalinou (liquid) a jinou tekutina (fluid) se tvoří rozhraní s určítou povrchovou nebo mezifázovou energií, na přechodu je mezifázová vrstva velikosti jednotek až desítek nm, v níž se mění koncentrace z hodnot jedné do hodnot druhé fáze. Rozhraní má proměnný tvar takový, aby byla co nejmenší celkové energie soustavy. Měřítkem síly vedoucí systém do tohoto stavu je povrchové nebo mezifázové napětí
Mezi pevnou látkou (solid) a tekutinou (fluid) má rozhraní pevný tvar, povrch má určitou povrchovou a mezifázovou energii. Je-li tekutinou kapalina, podle velikosti energií může smáčet či naopak
Rozhraní mezi dvamě pevnými látkami má pevný tvar, který nemusí odpovídat okamžité rovnováze, a mezifázovou energii.
Na rozhraní mezi tekutými fázemi existuje mezifázová vrstva, ve které se mění vlastnosti směsi z hodnot odpovídajících jedné fázi na hodnoty fáze druhé [3]. Tloušťka této vrstvy je obvykle řádu jednotek až desítek nm. Veličiny zde mají gradient kolmo k rozhraní, uvnitř fází jsou homogenní, odhlédneme-li od fluktuací. Hodnoty extensivních veličin v soustavě s fázovým rozhraním mohou být jiné, než je součet těchto veličin v odpovídajících objemech uvnitř objemových fází. Poměry tohoto rozdílu k ploše fázového rozhraní se označují jako povrchové a mezifázové veličiny.
K veličinám, jejichž změna v mezifázové oblasti je nejčastěji sledována, patří koncentrace složek (jim odpovídající povrchovou veličinou je povrchový přebytek), hustota a tlak (jemu odpovídá povrchové či mezifázové napětí).
Jednou z nejlépe pozorovatelných zvláštních vlastností povrchů je povrchové napětí. Povrchové napětí je měřitelná síla, která existuje na všech kapalných površích. Pramení z nesymetrického působení kohesních sil na molekuly v povrchové, popř. mezifázové vrstvě. Jeho existence se projevuje v tom, že se kapalina chová podobně, jako by byla potažena pružnou blánou, a ve schopnosti kapaliny smáčet. Velikost povrchového napětí se pohybuje u běžných kapalin zpravidla v rozmezí desítek mN.m-1.
K pojmu povrchového napětí lze dospět několika způsoby: popisně pomocí mechaniky spojitého prostředí, dále příčinně pomocí mechaniky na úrovni částic, a konečně pomocí makroskopické termodynamiky, kde se však vlastně jedná o volnou povrchovou energii, která je s povrchovým napětím svou velikostí i rozměrem shodná.
Odvození povrchového napětí z pohledu mechaniky spojitého prostředí uvádí v precizní formě Goodrich [1]:
Tlak je obecně popsán symetrickým tensorem 2.řádu, tj. o 6 různých prvcích. V isotropním prostředí (objemová fáze) si jsou diagonální složky rovné a ostatní jsou nulové. O mezifází se předpokládá,že je válcově symetrické kolem osy kolmé na fázové rozhraní. Z podmínky invariance tenzoru tlaku vůči rotaci kolem osy symetrie plyne, že nediagonální složky budou nulové, diagonální složky pT kolmé na osu symetrie si budou rovné a nezávislé na složce osové pN. Podmínkou mechanické rovnováhy je:
| ¶pT /¶x = ¶pT /¶y = 0; ¶pN /¶z = 0 | (1) |
kde x,y,z jsou kartézské souřadnice.
Složka pN tedy musí být v mezifázové vrstvě stejná jako v objemové fázi a je ztotožnitelná s hydrostatickým tlakem. Práce potřebná na deformaci takového systému popsanou tenzorem E o složkách eij je
| d W = |
(2) |
Protože v objemové fázi je tato práce
| d W =
p |
(3) |
lze rovnici přepsat
| d W = pN d V - g dA | (4) |
kde g = ![]() (pN-pT)
dz a d A =
(pN-pT)
dz a d A = ![]() (exx+eyy)dx
dy.
(exx+eyy)dx
dy.
Veličina se pak nazývá povrchové (mezifázové) napětí. V značí objem, A plochu.
Povrchová energie odpovídá reversibilní práci, které je zapotřebí na vytvoření jednotkového povrchu:
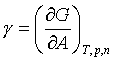 |
(5) |
V systémech s anizotropním povrchem, u kterých není splněna podmínka symetrie požadovaná pro platnost uvedeného odvození, se rozlišují dvě veličiny: tenzorová (surface stress), reprezentující sílu k roztažení existujícího povrchu, a skalární (surface tension), představující práci na tvorbu jednotkové plochy nového povrchu [2].
Povrchová vrstva se vyznačuje odlišností některých veličin od hodnot uvnitř fází. K jejich vystižení byly zavedeny tzv. povrchové a mezifázové veličiny, které vyjadřují, oč je příslušná veličina v systému s jednotkovou plochou fázového rozhraní větší, než by byl součet takových hodnot pro izolované fáze. Povrchová vrstva (mezifází) se vymezuje např. [3] jako oblast konečné tloušťky (obvykle do 0.1 μm), ve které se mění vlastnosti směsi z hodnot odpovídající jedné fázi na hodnoty fáze druhé. Veličiny zde mají gradient kolmo k mezifází, v objemu jsou homogenní.
Povrchové a mezifázové veličiny lze z termodynamických funkcí odvodit např.takto [1]:
Nechť jsou veličiny označeny obvyklým způsobem, tj. S je entropie, V objem, A povrch, n látkové množství, T teplota, p tlak, chemický potenciál, E (U) vnitřní energie, R plynová konstanta, k Boltzmannova konstanta. Horní pravé indexy nechť označují fázi, dolní pravé složku, ke které se příslušná veličina vztahuje, pruh nad symbolem parciální molární veličinu. V jednosložkovém systému je Gibbs-Duhemova rovnice pro každou fázi převoditelná do tvaru s molárními veličinami qM:
| SMjdT - VMjdp + d μ= 0 j = α,β | (6) |
a pro celý systém platí:
| SdT - Vdp + Adγ + ndμ = 0 | (7) |
Vynásobením rovnic (6) pro fáze α,β libovolnými multiplikátory x,y a odečtením od (7) vzniká:
| (S-xSMα -ySMβ )dT - (V-xVMα -yVMβ )dp + A dγ + (n-x-y)dμ =0 | (8) |
kdy volbou x a y tak, že platí:
| x + y = n xVMα + yVMβ = V | (9) |
lze získat výraz pro teplotní derivaci
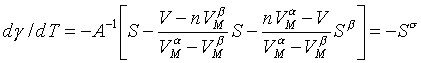 |
(10) |
Ukazuje se, že x a y představují přibližně látková množství složky v jednotlivých fázích a veličina SσM entropii tvorby jednotkového povrchu. Kombinací rovnic
| EjM = TSjM - pVjM + μ | (11) |
s rovnicí pro celkovou energii soustavy
| E = TS - pV + γA + n μ | (12) |
vzniká rovnice pro povrchovou energii (surface excess energy):
| Eσ = TSσ + γ | (13) |
kde
| Eσ = A-1(E - xEα - yEβ ) | (14) |
Rovnice (13) je analogická Gibbs-Helmholtzově rovnici pro objemovou fázi. pak odpovídá Helmholtzově Fσ , popř. Gibbsově Gσ energii tvorby povrchu; jelikož došlo při odvození k eliminaci členu pV, mizí u povrchových veličin rozdíl mezi energií a entalpií.
Pokud se pro stejné odvození užije v rovnici (6) objemových veličin místo molárních, volí se multiplikátory x,y tak, že x+y=V, x.sα +y.sβ =S. Pak x a y představují přibližné objemy fází Vα, Vβ. Analogickým postupem se dojde k nové veličině
| Γ= A-1 (n - Vαcα- Vβcβ) | (15) |
nazvané povrchový přebytek a představující rozdíl látkového množství složky v soustavě s fázovým rozhraním a součtu jeho j hodnot ve fázích α,β , vztažený na jednotku povrchu. cj je koncentrace složky ve fázi j.
Obdobným postupem z Gibbs-Duhemovy rovnice pro dvousložkový systém
| SdT - Vdp + Adγ + n1dμ1 + n2dμ2= 0 | (16) |
získáme veličinu
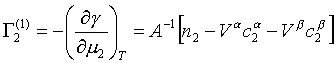 |
(17) |
Podobně 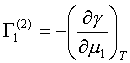 , přičemž jsou oba přebytky navzájem vázány
vztahem:
, přičemž jsou oba přebytky navzájem vázány
vztahem:
| (18) |
Zjednodušené odvození některých rovnic pro vícesložkový systém uvádí Wu [3]:
Platí podmínka rovnováhy (chemické potenciály jednotlivých složek nezávisejí na fázi), proto platí rovnice:
| d Gj = -Sj dT + Vj dp + μ1dnj1 + μ2dnj2 | (19) |
| d Gσ = -Sσ dT + Vσ dp + μ1dnσ1 + μ2dnσ2 | (20) |
přičemž jsou celkové Gibbsovy energie
| Gj = nj1 μ1 + nj2 μ2 Gσ = nσ1 μ1 + nσ2 μ2 | (21) |
| a Gσ /A = fσ = γ+ Γ1 μ1+ Γ2 μ2 | (22) |
kde Γi odpovídá Γi(j) v rovnici (17).
Z Gibbs-Duhemovy rovnice pro povrchovou vrstvu tloušťky l
| Sσ /A dT - ldp + dγ+ Γ1dμ1+ Γ2 dμ2 = 0 | (23) |
dostáváme derivací podle teploty a dosazením dμi = Vi dp-SidT,
kde se parciální molární veličiny vztahují k celému systému:
| -dγ /dT = (S- Γ1S1 - Γ2S2) - (l- Γ1V1 - Γ2V2) dp/dT | (24) |
kde obsah první závorky je entropie tvorby mezifází vztažená na jednotku povrchu ΔSσP
Entalpie tvorby mezifází je ΔHσL = - T dγ /dT a latentní teplo tvorby mezifází je ΔFσL =-T dγ /dT.
Pomocí této teorie se počítá povrchová energie, která se u jednosložkových systémů ztotožňuje s povrchovým napětím.
Je-li potenciální energie mezi dvěma molekulami kapaliny dána Lennard-Jonesovým potenciálem
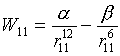 |
(25) |
(α a β jsou silové konstanty), lze povrchovou energii, tj.energii potřebnou na oddělení dvou nekonečných bloků o jednotkové styčné ploše, odhadnout na
|
(26) |
kde r0 značí vzdálenost částic v nejbližších vrstvách obou bloků.
Pro styk kapaliny a páry, kde r0 aproximujeme polovinou vzdálenosti molekul v kapalině rL , se tato energie mění na
 |
(27) |
a povrchové napětí je γ= WLV/2, neboť vypočtená energie se vztahuje k dvojici povrchů. NL je početní koncentrace částic v kapalné a NV v plynné fázi.
Povrchové napětí lze rozložit na příspěvky γd působené dispersními silami mezi částicemi a γp sil polárních (permanentní a indukovaný dipol, vodíková vazba). K charakterizaci podílu polární složky sil slouží veličina γp /(γd+γp) zvaná polarita. Polarita polymerů byla shledána nezávislou na teplotě [3]. Nulovou polaritu má polyethylen, vysokými hodnotami se vyznačují např. polymethylmethakrylát (0.28), polyethylenoxid (0.28), polyvinylacetát (0.33).
Z předchozího plyne, že povrchové napětí je svázáno s jinými veličinami závislými na konstantách silového působení mezi částicemi a na vzdálenosti mezi nimi. Např. kompresibilita æ definovaná
| æ = - (d ln V/dp)T | (28) |
je s ním svázána vztahy
| æ.γ4/3 = 0,00233 | (29a) |
nebo
| æ.γ4/3 = 1,2.10-3 T-1/3 | (29b) |
Z porovnání práce nutné k přemístění molekuly na povrch kapaliny s výparným teplem L získáváme nepřesnou, ale názornou rovnici γ.(Vi)2/3 = HLi/2 , kde Vi a HLi jsou objem a výparné teplo připadající na jednu molekulu [4].
V termodynamice se pro popis některých soustav používá redukovaných veličin. Analogicky k redukovanému tlaku, objemu a teplotě lze zavést i redukované povrchové napětí [3]
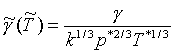 |
(30) |
přičemž ~ označuje redukovanou veličinu a * redukční parametr (q~ = q/q*). Redukované povrchové napětí je funkcí redukovaného objemu V~, jeho závislost se často popisuje rovnicí
 |
(31) |
Tangenciální složky povrchového napětí se kompenzují jen na rovném rozhraní. Na rozhraní zakřiveném existuje rozdíl tlaků.
Názorný výklad tohoto jevu podává Padday [4]:
Mějme element zakřiveného povrchu s hlavními poloměry křivosti R1 a R2 , jak je znázorněno na obr.1. Označme délku strany x1y1 jako a a strany xx1. Jeho plocha je A=a.b. Práce na jeho posunutí proti kolmému tlaku p je W = Δp dV =Δp ab dz. Tato práce je konána proti povrchovým silám, které konají práci W = γdA = γ.d(ab).
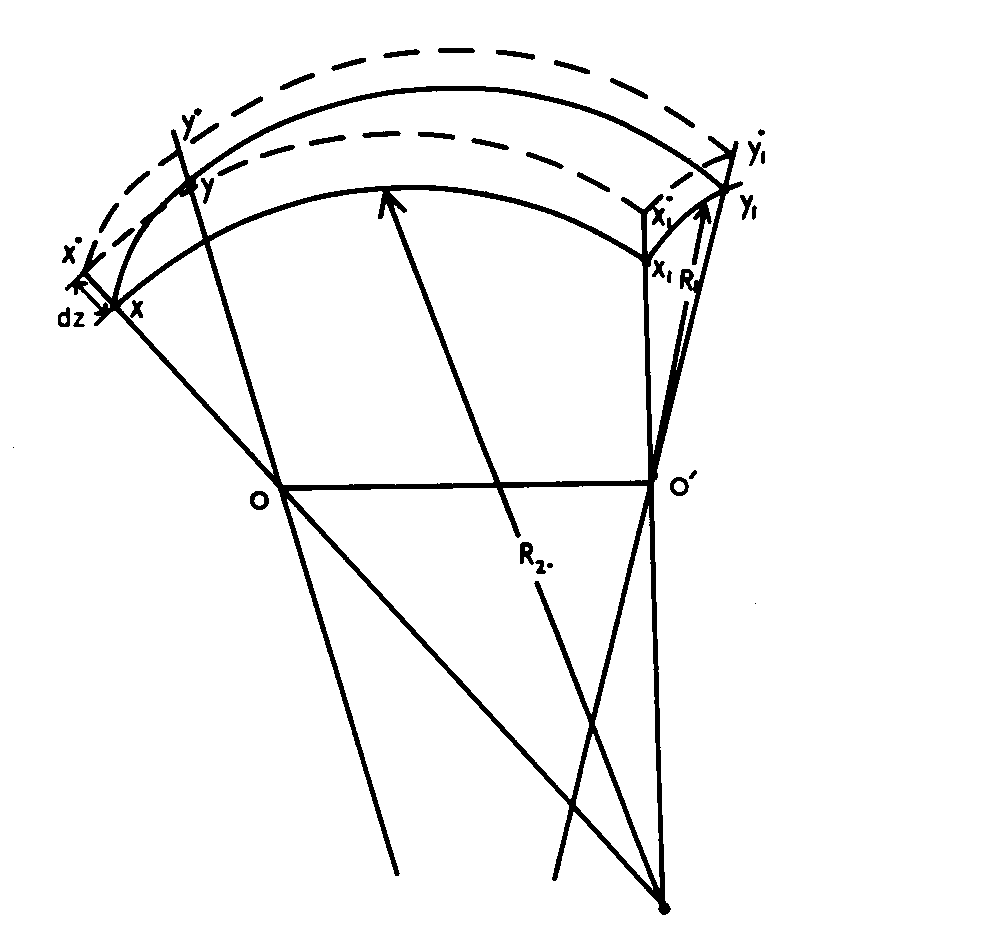
Obrázek 1: Element zakřiveného povrchu s hlavními poloměry křivosti r1 a r2 [4]
Z rovnosti těchto dvou prací máme pro rozdíl tlaků
| Δp = γ.d(ab) / abdz = γ (da/adz+db/bdz) | (32) |
a poněvadž na základě podobnosti platí
| da / dz = a / r1 | db / dz = b / r2 | (33) |
je
Δp = γ (1/r1+1/r2) |
(34) |
Přesné odvození uvádí Goodrich [1]. V něm se ukazuje, že podmínkou platnosti vztahu je, aby změna tečné složky tlaku pT podél povrchu byla zanedbatelně malá.
Při velkém zakřivení klesá povrchové napětí. Např. Tolman [5] odvodil vztah
| γ0/γ = 1 + 2t/r | (35) |
kde t je tloušťka mezifázové vrstvy a r poloměr zakřivení. s
Doporučeny dále tyto články z textu doc. Lidmily Bartovské a doc. Marie Šiškové: