Jak bylo zmíněno v přehledu metod, jsou pro určování povrchového a mezifázového napětí polymerů nejvhodnější metody, které vycházejí z tvaru rozhraní. Teoreticky vycházejí z rovnice pro povrchy válcově symetrické v homogenním tíhovém poli. Na zakřiveném rozhraní je na vnitřní straně povrchu přetlak (rov.34)
| (42) |
kde ci jsou jeho hlavní křivosti (ri poloměry křivosti).
V homogenním tíhovém poli o zrychlení g pak rovnice pro zakřivení rozhraní mezi prostředími o hustotách ρ1 a ρ2 v bodě daném souřadnicí z ve směru osy symetrie přechází na:
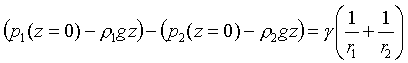 |
(43) |
což nabývá vyjádřením rozdílu veličin q: Δq = q2- q1 podoby
| (44) |
kde Δp je rozdíl tlaků v místě nulové souřadnice z, která se umisťuje do průsečíku osy symetrie s tečnou rovinou plochy fázového rozhraní kolmou na tuto osu, r1 a r2 jsou poloměry křivosti orientované na stranu fáze 1.
Při této volbě je pak Δp = 0 v případě rozhraní
typu vlákna čnícího kolmo z kapaliny (z = 0 odpovídá
volné hladině), nebo![]() v případě kapek,
bublin, menisků v kapiláře apod., přičemž b = r1
(z=0) = r2 (z=0) je poloměr křivosti ve
vrcholu kapky (menisku), z=0 odpovídá vrcholu kapky.
Visící kapku znázorňuje obr.2.
v případě kapek,
bublin, menisků v kapiláře apod., přičemž b = r1
(z=0) = r2 (z=0) je poloměr křivosti ve
vrcholu kapky (menisku), z=0 odpovídá vrcholu kapky.
Visící kapku znázorňuje obr.2.
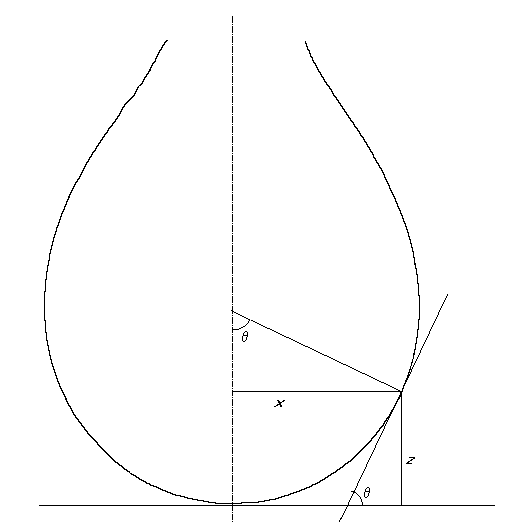
Obrázek 2: Visící kapka a její zakřivení
V tomto druhém případě přechází rovnice (44) do tvaru
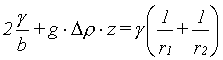 |
(45) |
Člen na pravé straně lze přepsat jako
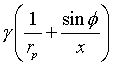
kde rp je poloměr křivosti meridianové křivky kapky, Φ je úhel normály povrchu kapky s osou symetrie, přičemž x je souřadnice kolmá k ose symetrie.
Zavedeme-li bezrozměrné proměnné tvaru Z =z/b a X = x/b ,je
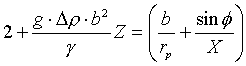 |
(46) |
Fyzikální veličiny vystupují v jediném parametru, značeném
obvykle 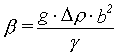 (např.J.F.Padday [4] na str. 83
). Takto definovaná hodnota β je pro visící kapku
záporná, pro sedící kladná. Často se také symbolem β
značí hodnota opačného znaménka (např.Ambwani[8]). Rovnice (46) se dá vyjádřit
pomocí derivací dle parametru t, jehož funkcí jsou X,
Z a Φ.:
(např.J.F.Padday [4] na str. 83
). Takto definovaná hodnota β je pro visící kapku
záporná, pro sedící kladná. Často se také symbolem β
značí hodnota opačného znaménka (např.Ambwani[8]). Rovnice (46) se dá vyjádřit
pomocí derivací dle parametru t, jehož funkcí jsou X,
Z a Φ.:
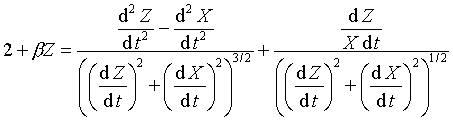 |
(47) |
V literatuře se nejčastěji prezentuje s parametrem t=X:
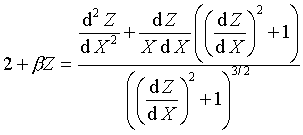 |
(48) |
což je ale pro výpočet naprosto nevhodné, neboť většině X příslušejí dvě hodnoty Z a derivace Z podle X není všude konečná. Pro výpočty je výhodnější použít rovnice ve tvaru [9,10]
| (49) |
kde ![]() ,
, ![]()
a S je oblouk od vrcholu kapky.
Analogické jsou rovnice
| (50) |
| (51) |
Někteří autoři [11] užívají
pro převedení rovnice (45) do bezrozměrného tvaru parametru c
= 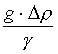 a
parametry jsou pak definovány X = x.c1/2,
Z = z.c1/2 , B = b.c1/2
(což je β1/2) a rovnici (49) pak odpovídá
a
parametry jsou pak definovány X = x.c1/2,
Z = z.c1/2 , B = b.c1/2
(což je β1/2) a rovnici (49) pak odpovídá
| (52) |
Při kontrolním výpočtu pro β= 0 (kružnice) s krokem S 0,0001 dávala první rovnice výsledky přesnosti asi 0,000001, druhé dvě přesnosti asi 0,001.
Rovnici obdobnou (46), kde místo zakřivení profilu vystupuje objem V části kapky pod bodem, pro nějž je vyjadřována, odvodil Padday [12]:
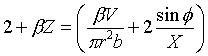 |
(53) |
Tato rovnice je vhodná spíše při numerickém zpracování tím, že místo derivací obsahuje integrovanou veličinu (objem), kterou lze zjistit z profilu kapky. Pro zpracování výsledků uvádí příklad jejího použití Girault [13].
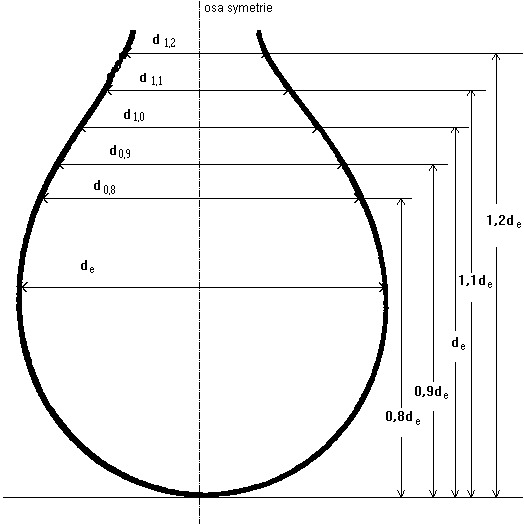
Obrázek 3: Vyhodnocování tvaru visící kapky
Měřit zakřivení ve vrcholu kapky by činilo potíže, proto se definuje výhodnější parametr H, definovaný:
| (54) |
kde de je maximální průměr kapky. Mezi H a β je vztah:
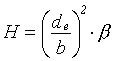 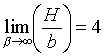 |
(55) |
Pro měření povrchového napětí se zjišťují vhodné rozměry kapky, které jsou voleny tak, aby byly vzájemně jednoznačnou funkcí parametru β. Tuto podmínku splňují například poměry průměru kapky dk v rovinách, vzdálených od vrcholu o k-násobek maximálního průměru, k tomuto maximálnímu průměru de (metoda vybrané roviny), značené Sk = dk/de . Základní hodnota k je 1, pro kterou se hodnota průměru d1.0 označuje ds, rozsah používaných k je od 0.8 do 1.2. Odečítání de a ds znázorňuje obrázek 3.
Pro vyhodnocení povrchového napětí se pomocí tabulek H - Sk určí H odpovídající naměřeným poměrům Sk . Z něj se vypočítá povrchové napětí. Jak patrno ze vzorce, je k výpočtu zapotřebí i znalosti hustoty vzorků. Jsou-li hodnoty H určené z různých rovin stejné, je to známka rovnováhy [14,15].
Zmíněné tabulky se získávají výpočtem křivek odpovídajících jednotlivým hodnotám parametru β.
Fordhamovy a Staufferovy [16] tabulky 1/H - S1.0 uvádí např. Padday [4] a Ambwani [8], ukázku pro S1.2 Roe [15]. Z důvodu uvedených v kapitole věnované vyhodnocování výsledků byly počítány vlastní tabulky pro k 0,8 až 1,2, které jsou uvedeny v příloze. Podle Roea [15] je ke zpracování tvarů visících kapek určených s běžným rozlišením zapotřebí přesnosti tabulek na 4.desetinné místo.
Výsledky integrace lze pro snadnější zpracování zejména výpočetní technikou s určitou nepřesností nahradit rovnicemi aproximujícími závislost H na S. Jednodušší z nich jsou typu 1/H = ke.S-km , přesnější mají tvar
| 1/H = ke .S-km + k3S3 + k2 S2 + k1S + k0 | (56) |
jak to udělal Misak [17].
Tabulka: koeficienty Misakových rovnic
| interval S | k0 | k1 | k2 | k3 | ke | km | |
| od | do | ||||||
| 0,9 | -0,20970 | -0,18341 | 1,08315 | -0,69116 | 0,30715 | 2,84636 | |
| 0,9 | 0,68 | -0,05877 | 0,14701 | -0,09155 | 0 | 0,31345 | 2,64267 |
| 0,68 | 0,59 | -0,05285 | 0,15756 | -0,11714 | 0 | 0,31522 | 2,62435 |
| 0,59 | 0,46 | -0,13261 | 0,50095 | -0,46898 | 0 | 0,31968 | 2,59725 |
| 0,46 | 0,40 | -0,18069 | 0,84059 | -0,97553 | 0 | 0,32720 | 2,56651 |
Kromě vyhodnocení tvaru kapky pomocí vybraných rovin jej lze hodnotit pomocí maximálního a minimálního průměru kapky (tj.průměru rovníku a krčku); příklad uvádí Winkel [18]. Výhodou je vzájemná nezávislost hodnot, nevýhodou obtížná lokalizovatelnost krčku.
Následující odstavce se zabývají tím, jak se do konečných výsledků měření metodou visící kapky a vybrané roviny promítá experimentální chyba
Pro chybu určení veličiny, jež je funkcí veličin qi nezávisle měřených s chybami dqi platí [8]:
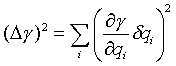 |
(57) |
V případě diskutovaného měření nabývá rovnice (57) tvaru
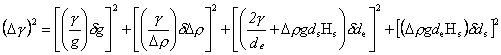 |
(58) |
kde 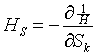
Relativní chyba je vyjádřena [8] rovnicí:

|
(59) |
Za předpokladu, že měření všech rozměrů vykazuje stejnou chybu δd, lze rovnici(59) upravit do tvaru
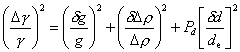 , ,
|
(60) |
kde 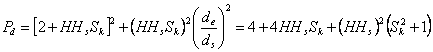 |
Hodnoty, kterých nabývá výraz Pd, jsou pro k = 1 vypsány v tabulce 2.
Tabulka 2: Hodnoty činitele příspěvku relativní chyby měření rozměrů P pro vybranou rovinu s koeficientem 1,0:
| S | 0 | 0,30 | 0,40 | 0,50 | 0,60 | 0,68 | 0,70 | 0,80 | 0,90 | 0,96 | 1,00 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Pd | ∞ | 99,5 | 65,3 | 49,4 | 40,7 | 36,4 | 35,5 | 32,4 | 30,9 | 30,6 | 30,7 |
Pro vyvinutou kapku nepolární látky bývá S kolem 0.9, pro nevyvinutou kolem 0.8; pro vyvinutou kapku vody kolem 0.6 a málo vyvinutou až kolem 0.5. Rovnice (60) spolu s tabulkou 2 ukazují, že při stejných relativních chybách určení rozměrů, hustoty a tíhového zrychlení je druhá mocnina příspěvku chyby určení rozměrů k celkové chybě určení povrchového napětí 30 až 50 krát větší než jednotlivé příspěvky chyb určení ostatních veličin.
Vyhodnocován zpravidla bývá obraz kapky ve zvětšeném měřítku. Upravíme-li rovnici (54) tak, že vyjádříme velikost d pomocí velikosti obrazu D a zvětšení obrazu K :
| (61) |
přechází rovnice (60) na obdobný tvar:
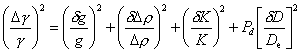 |
(62) |
která ukazuje, že na chybu převodu do správného měřítka je výsledná hodnota méně citlivá než vůči chybě určení parametrů tvaru.
Roe [15] při svém rozboru chyb ještě uvažuje dvě složky chyby měření ds: chybu určení vybrané roviny a vlastní chybu měření. Kvadrát chyby plynoucí z určení 1/H podle něj odpovídá:
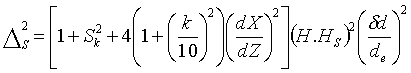 |
(63) |
Ve zvýšeném rozdílu mezi hodnotami povrchového napětí vypočítanými z rozměrů v jednotlivých vybraných rovinách, se mohou promítnout zejména následující faktory:
1. Chyby vzniklé při zobrazování kapky a proměřování obrazu:
a, Chyba určení maximálního průměru kapky
b, Chyba určení rozměru kapky v jednotlivých vybraných rovinách
2. Odchylky skutečného tvaru kapky od tvaru popsaného Bashforthovou - Adamsovou rovnicí (54) zapříčiněné nedokonalým splněním podmínek její platnosti, především mechanickou nerovnováhou.
K odhadnutí, zda chyba dle odst.1a působí, že se naměřená hodnota povrchového napětí posouvá systematicky podle vybrané roviny užité k vyhodnocování, byl proveden následující test:
Za základ byla vzata teoretická křivka, vypočtená pro parametr β= 0.25. Tato křivka byla vyhodnocována stejným způsobem jako měřené křivky s tím, že místo maximálního průměru byly dosazovány různé hodnoty lišící se oběma směry od skutečné hodnoty. Ostatní souřadnice křivky zůstaly nezměněny s tím, že byly zpracovávány s přesností na 3 platné číslice, což je praktická přesnost měření rozměrů kapky. Bylo sledováno, zda nastává závislost povrchového napětí na vybrané rovině. Ostatní modelové parametry byly zvoleny tak, aby se blížily hodnotám v reálných systémech. Výsledky shrnuje tabulka 3.
| Modelové parametry: | |
| β = 0.25 | 1/H = 0.90962 |
| b = 1.2195 mm | γ= 58.36 mN.m-1 |
| g = 9.8077 m.s-2 | max.průměr = 2.5573 mm |
| ρ= 1000 kg.m-3 |
Tabulka 3: Povrchová napětí zpětně získaná z teoretické křivky v závislosti na zkreslení hodnoty maximálního průměru. (v disertaci tab 3.7)
| Povrchové napětí/(mN m-1 ) | |||||
|---|---|---|---|---|---|
| max. průměr [m m] | 2,439 | 2,5365 | 2,557 | 2,561 | 2,683 |
| k = 0,8 | 25,14 | 49,37 | 58,16 | 60,03 | 381,8 |
| k = 0,9 | 32,04 | 52,16 | 58,27 | 59,67 | 136,7 |
| k = 1,0 | 37,01 | 53,79 | 58,40 | 59,23 | 98,0 |
| k = 1,1 | 41,06 | 54,91 | 58,42 | 58,97 | 82,9 |
| k = 1,2 | 44,36 | 55,72 | 58,40 | 58,84 | 74,9 |
| průměr | 35,9 | 53,2 | 58,33 | 59,35 | 155 |
| odchylka | 6,8 | 2,25 | 0,10 | 0,45 | 115 |
| d γ/ d k | 47,5 | 15,4 | 0,63 | -3,3 | -668 |
Pro maximální průměr kapky 2.5573 mm při přesnosti dosazování průměrů ve vybraných rovinách na 4 platná místa byla průměrná vypočtená hodnota povrchového napětí (58.37±0.01) mN.m-1 a směrnice dγ/dk -0.08 mN.m-1.
Uvedené výsledky ukazují, že chyby v určení maximálního průměru kapky se poměrně výrazně projevují v závislosti získaných hodnot na vybrané rovině.
Chyby uvedené pod bodem 1b lze pokládat za náhodné.
Chyby způsobené skutečnou deformací kapky představují nejdůležitější faktor ovlivňující použitelnost metody. Projevují se rozptylem hodnot naměřeného povrchového napětí a působí zpravidla i posun určené střední hodnoty povrchového napětí.
Z hlediska závislosti vypočtených hodnot povrchového napětí na použité vybrané rovině a velikosti jeho rozptylu lze uvažovat několik kombinací.
Je-li rozptyl větší, než by přicházelo v úvahu, kdyby byl způsoben jen chybou měření rozměrů obrazu, a není-li zjištěna závislost vypočtených povrchových napětí na rovině měření, jedná se zřejmě o skutečnou deformaci kapek, a to pravděpodobně lokálními deformacemi okolo rovnovážné polohy. Průměrná hodnota se pravděpodobně odlišuje od skutečné hodnoty povrchového napětí.
Nachází-li se kapka v nerovnovážném, ale relativně ustáleném stavu s válcovou symetrií, kterým prochází při ustavování rovnovážného stavu po vytlačení v prostředí bez rušivých vlivů, projevuje se závislost zjištěné hodnoty povrchového napětí na vybrané rovině podobným způsobem, jako efekt uvedený pod bodem 1a.
Vykazuje-li zjištěná hodnota povrchového napětí v naměřených hodnotách velký rozptyl a je-li zjištěna závislost vypočtené hodnoty na vybrané rovině, lze upravit údaj maximálního průměru na takovou hodnotu, aby byla odstraněna zmíněná závislost na vybrané rovině. Pokud i pak zůstane velká hodnota rozptylu, je kapka v nerovnovážném stavu, který není ani relativně ustálený, ani vzniklý lokálními deformacemi kolem rovnovážného stavu. Dosáhlo-li se podstatného snížení rozptylu, může se jednat o deformaci uvedenou v předchozím odstavci nebo o chybu určení maximálního průměru; takto získaný průměr však nemusí odpovídat skutečnému povrchovému napětí.
Nachází-li se kapka v nerovnovážném, ale relativně ustáleném stavu s válcovou symetrií, kterým prochází při ustavování rovnovážného stavu po vytlačení v prostředí bez rušivých vlivů, projevuje se závislost zjištěné hodnoty povrchového napětí na vybrané rovině podobným způsobem, jako efekt uvedený pod bodem 1a. Viskosní kapaliny zaujímají bezprostředně po vytlačení z kapiláry tvar vlákna, ze kterého zvolna přecházejí do tvaru řídícího se Bashforthovou - Adamsovou rovnicí (r2-135). Na počátku se všechny poměry Sk blíží jedné. Tomu odpovídá zjištění povrchového napětí menšího než je ve skutečnosti, obvykle s menšími hodnotami získanými z rovin vzdálenějších od vrcholu kapky. Pokud kapka ztrácí rovnováhu a směřuje k odkápnutí, vytváří se úzký krček, oproti rovnovážnému tvaru se zmenšují průměry řezů ve vybrané rovině, a to výrazněji ve větší vzdálenosti od vrcholu. Tomu odpovídá zjištění povrchového napětí většího než je ve skutečnosti, obvykle s největšími hodnotami získanými z rovin vzdálenějších vrcholu kapky
Jak se uvedené příčiny projevují na závislosti zjištěných povrchových napětí na relativní vzdálenosti vybrané roviny od vrcholu kapky a na odchylce naměřených hodnot povrchového napětí od hodnot skutečných shrnuje tabulka
Tabulka: Projev rušivých vlivů při měření povrchového napětí
| příčina | γexp-γskut | dγ/dk |
| nadhodnocení de | kladná | záporná |
| podhodnocení de | záporná | kladná |
| kapka před ustálením | záporná | záporná |
| odkapávající kapka | kladná | kladná |
Pro tuto kapitolu jsou dále doporučeny tyto články z knihy doc. Bartovské a doc. Šiškové: