Metody měření povrchového a mezifázového napětí založené
na měření síly
lze rozdělit na metody s přímým měření síly (či
tlaku) a nepřímým.
- Nepřímé měření síly
- Metoda měření výšky hladiny v kapiláře
(capillary rise)
- příbuzná metoda padajícího menisku
pro určení dynamického povrchového
napětí
- Určování povrchového napětí z váhy kapky
(stalagmometrie)
- Výtokové metody
- Přímé měření síly
- Metody Wilhelmyho destičky (Wilhelmy plate) a de
Noüyova prstence (de Noüy ring)
- Metoda maximálního tlaku v bublině (maximum
bubble pressure)
Metoda měření výšky hladiny v kapiláře (capilary rise)
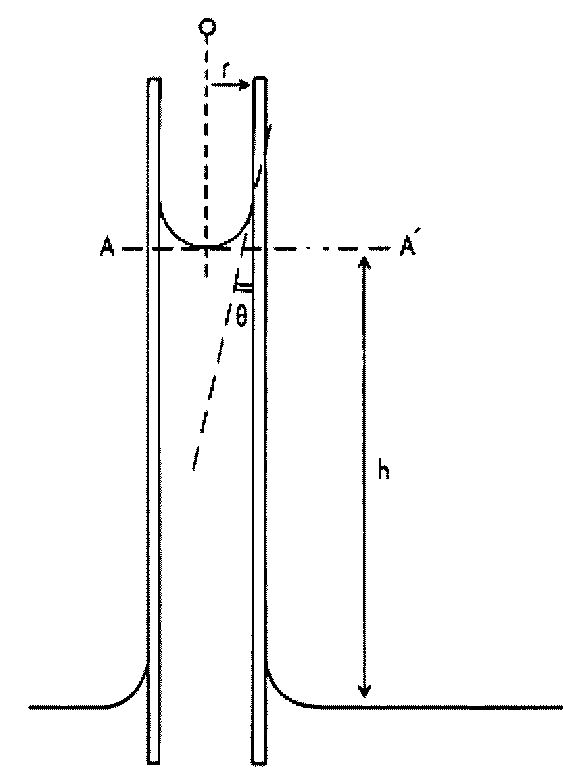 je nejstarší metodou měření
povrchového napětí. Využívá rovnováhy mezi povrchovou
silou 2π r γ.cosθ (r je vnitřní poloměr
kapiláry, θ kontaktní úhel měřené kapaliny na
materiálu kapiláry) a tíhou kapaliny ve sloupci ρgh.
Pro povrchové napětí pak platí γ=ρgrh /2cosθ .
(obrázek z [4])
je nejstarší metodou měření
povrchového napětí. Využívá rovnováhy mezi povrchovou
silou 2π r γ.cosθ (r je vnitřní poloměr
kapiláry, θ kontaktní úhel měřené kapaliny na
materiálu kapiláry) a tíhou kapaliny ve sloupci ρgh.
Pro povrchové napětí pak platí γ=ρgrh /2cosθ .
(obrázek z [4])
Výhodou metody je jednoduchost, nevýhodami potřeba znát
hustotu, kontaktní úhel (což lze kompenzovat měřením ve
dvou kapilárách různého průměru, ale při nižší přesnosti),
závislost na materiálu kapiláry a pro přesná měření
velké nároky na čistotu, rovnoměrnost, kruhovost a přesnost
průřezu kapiláry, a dále nutnost provádět korekce na přesný
objem v okolí menisku. Při uplatnění korekcí je však jednou
z nejpřesnějších absolutních metod.
Metoda výšky hladiny v kapiláře je omezena dobou ustavení
mechanické rovnováhy, kterou prodlužuje jednak hystereze smáčení,
jednak viskozita. U viskosních kapalin trvalo dosažení
rovnováhy týdny (Edwards [7] uvádí 4 týdny pro kapalinu o 10
kPa.s (105 P)), zatímco u visící kapky uvádí Wu
[6] při viskozitě 107-108 P ( 1-10 MPa.s)
dobu asi 30 minut (z prací Roea a svých).
Není-li znám kontaktní úhel, lze potřebu jeho znalosti
obejít měřením ve dvou kapilárách různého průměru. To
ale snižuje přesnost.
Pro popis menisků byla zavedena kapilární konstanta a
rovnicí a2=2γ/ρg. Obecnější postup je pak
takový, že z geometrie menisku je určována kapilární
konstanta, z níž se pak vypočítá povrchové napětí.
Pro kapilární konstantu jsou v literatuře [4] uváděny tyto rovnice:
| Malé trubice |
Klasická |
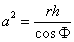 |
| Jurin |
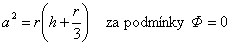 |
| Střední trubice |
Rayleigh |
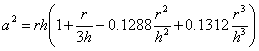 |
| Rayleigh |
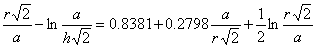 |
| Všechny |
Bashforth a Addams |
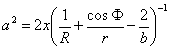 |
| Bashforth a Addams, Padday |
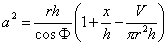 |
| Laplace |
a2=bh |
Korekcí vycházejí z toho, že pomocí tabelovaných hodnot
závislosti mezi r/b a r/a lze z
geometrie menisku (experimentálně zjištěného poměru r/h)
určit kapilární konstantu, z níž je určeno povrchové či
mezifázové napětí.
- Výchozí odhad je: r/a=(r/h)1/2 Z
něj se najde odpovídající r/b podle tabulek k
danému r/a
- Pro další odhady se vždy k předchozímu poměru r/a
najde v tabulkách odpovídající r/b a určí
se zpřesněné r/a: (r/a)n=(r2/hb)1/2=
(r/h)1/2 (r/b)1/2
Protože poloměr kapiláry je znám, lze numerickou
integrací Youngovy-Laplaceovy rovnice 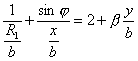 , v níž
, v níž 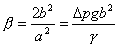 , získat závislost podílu h/r
na tvarovém činiteli, zde E0 definovanému
, získat závislost podílu h/r
na tvarovém činiteli, zde E0 definovanému 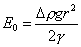 ,rovnici
,rovnici
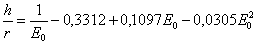 .
.
Diferenciální 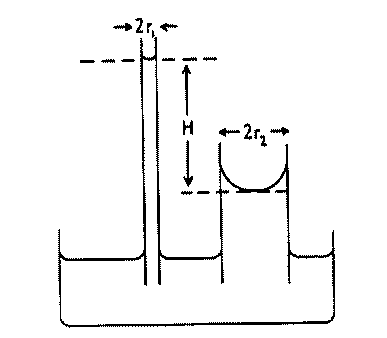 měření znázorňuje obrázek
z publikace [4], přičemž platí H=a2(1/b1-1/b2)
.
měření znázorňuje obrázek
z publikace [4], přičemž platí H=a2(1/b1-1/b2)
.
Pro přesnost měření je třeba dbát na
- průměr vnější nádoby >8cm (aby nebyla ovlivněna
volná hladina)
- pečlivé měření průměru kapiláry (Hg kapky)
- kruhový průřez kapiláry
- polohu volné hladiny pozorovat jehlou těsně u povrchu
(přiblížení jehla+odraz)
- čistotu trubička, nulový kontaktní úhel, měřit
meniskus po smočení stěn kapiláry
- měření přesným katetometrem nebo optickým zařízením,
vyloučení vibrací
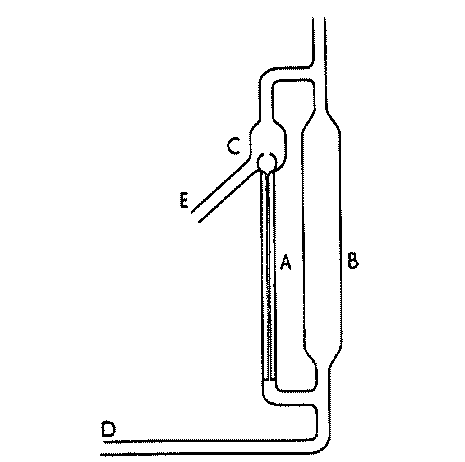 Padday [4] zmiňuje
ještě Youngovu a Grossovu aparaturu:
Padday [4] zmiňuje
ještě Youngovu a Grossovu aparaturu:
Kapilára A průměru 0.25 mm pro vodu
Trubice B průměr přes 8 cm
kapalina přiváděna trubicí D
vytlačením a přetečením z C do E obnoven povrch měřené
kapaliny, takže je měřen čerstvý.
Doporučeny dále tyto články z textu doc. Lidmily
Bartovské a doc. Marie Šiškové:
http://vydavatelstvi.vscht.cz/knihy/uid_es-001/hesla/kapilarni_deprese.html
, http://vydavatelstvi.vscht.cz/knihy/uid_es-001/hesla/kapilarni_elevace.html
, http://vydavatelstvi.vscht.cz/knihy/uid_es-001/hesla/metody.kapilarni_elevace.html
Metody Wilhelmyho destičky (Wilhelmy plate) a de Noüyova
prstence (de Noüy ring)
zjišťují povrchové napětí pomocí síly působící na předmět,
který se dotýká hladiny kapaliny. V prvním případě je jím
destička a měří se síla v klidu, ve druhém případě
prstenec a měří se maximální síla při jeho vytahování určitou
rychlostí. Výhodou metod je, že není zapotřebí znát
hustotu měřené kapaliny. Na druhé straně musí být
kontaktní úhel na tělese nulový nebo alespoň známý. Metoda
prstencová je vzhledem k tomu, že není klidová, nevhodná k měření
směsí a roztoků povrchově aktivních látek jakož i viskosních
kapalin a je třeba provádět korekce; přesto je však metoda základem
některých komerčních přístrojů.
Dále doporučeno: http://vydavatelstvi.vscht.cz/knihy/uid_es-001/hesla/metody.vyvazovani_desky.html
, http://vydavatelstvi.vscht.cz/knihy/uid_es-001/hesla/metody.odtrhavaci_metody.html
Metoda maximálního tlaku v bublině (maximum bubble
pressure)
využívá znalosti průběhu tlaku v bublině při jejím
vytlačování z ponořené trubičky do kapaliny. Pro přesné měření
je opět zapotřebí korekcí; nelze měřit viskozní kapaliny a
směsi.
http://vydavatelstvi.vscht.cz/knihy/uid_es-001/hesla/metody.maximalni_pretlak.html
Určování povrchového napětí z váhy kapky
(stalagmometrie)
je založeno na rovnováze povrchové síly 2πrγ a
tíhy kapky mg. r je poloměr průřezu kapky v místě,
kde dochází k přetržení. V hrubém přiblížení se předpokládá
jeho shoda s poloměrem otvoru, z kterého kapka visí. Metoda je
v jednoduchém uspořádání nenáročná na experimentální
vybavení, je však třeba korekcí na skutečný průměr
krčku. Metoda je nepoužitelná na příliš viskosní látky,
směsi a roztoky povrchově aktivních látek.
Při měření elektrokapilárních křivek rtuti touto
metodou byla objevena polarografie
http://vydavatelstvi.vscht.cz/knihy/uid_es-001/hesla/metody.stalagmometrie.html
Výtokové metody
Rovnováha kapilárních a gravitačních sil při výtoku z
úzké trubice
a) kritický průměr, na kterém se zastaví kapka lehčí
kapaliny v konické trubici
b) kritický úhel náklonu, při kterém se kapka zastaví
Doporučeny dále tyto články z textu doc. Lidmily
Bartovské a doc. Marie Šiškové: http://vydavatelstvi.vscht.cz/knihy/uid_es-001/hesla/metody.elevace_na_desce.html
Dynamické povrchové napětí - metoda padajícího menisku
Metoda je určena pro stáří povrchu v sekundách až
několika minutách.
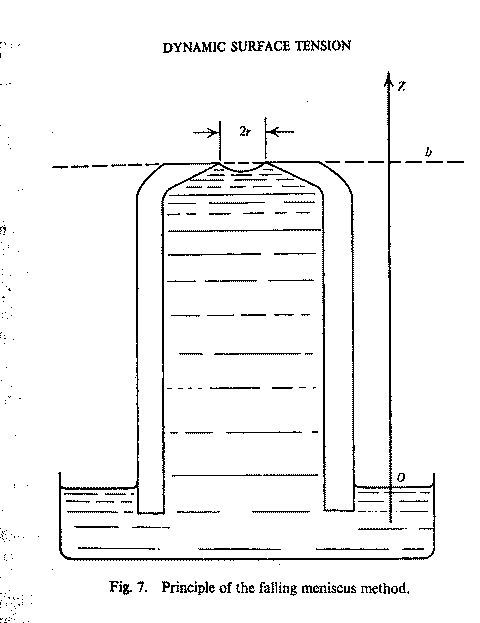
Princip ukazuje vyobrazení z Defayovy monografie [104]: Na povrchu nekapilární trubice je
malý kruhový otvor poloměru r. Trubice je ponořena
do kapaliny tak, že otvor má výšku h nad volnou
hladinou, je přitisknut k hraně. V mechanické rovnováze
platí rovnice:
 , kde R je poloměr hlavní křivosti
ve výšce Z. Podmínka, aby meniskus držel, je R=>r.
Pro daný poloměr otvoru a výšku je k udržení kapaliny v
trubce potřeba povrchového napětí minimálně takového, aby
bylo R=r.
, kde R je poloměr hlavní křivosti
ve výšce Z. Podmínka, aby meniskus držel, je R=>r.
Pro daný poloměr otvoru a výšku je k udržení kapaliny v
trubce potřeba povrchového napětí minimálně takového, aby
bylo R=r.
Postup měření:
- V čase t=0 vytvořen čerstvý povrch ve výšce h1
- Kapalina drží v trubici, dokud povrchové napětí
nepoklesne pod γ1.
- Postupně se mění výšky a měří čas, při kterém
z každé z nich hladina spadne.
- Přesnější vzorec je
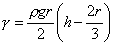
Podmínky měření:
- Vytvořit skutečně čerstvý povrch na počátku
- pokud možno se vyhnout pohybům, které jej mohou znečistit
nebo rozšířit - smočit další plochu.
Metoda padajícího menisku - aparaturu ukazují vyobrazení
opět z monografie [104]:

Odsáváním se naplní nádoba A a kapalina přetéká skrz
T. Snížením tlaku se hladina sníží mezi h a hr.
Otevře se kohoutek R.: meniskus se rychle přemístí z 1 do 2,
vyteče trochu kapaliny z otvoru. Když meniskus 2 dosáhne
vrcholu trubice, kohoutek R se zavře a začne se měřit čas,
obnoví se atmosférický tlak v A a F.
Zpět na seznam témat
 je nejstarší metodou měření
povrchového napětí. Využívá rovnováhy mezi povrchovou
silou 2π r γ.cosθ (r je vnitřní poloměr
kapiláry, θ kontaktní úhel měřené kapaliny na
materiálu kapiláry) a tíhou kapaliny ve sloupci ρgh.
Pro povrchové napětí pak platí γ=ρgrh /2cosθ .
(obrázek z [4])
je nejstarší metodou měření
povrchového napětí. Využívá rovnováhy mezi povrchovou
silou 2π r γ.cosθ (r je vnitřní poloměr
kapiláry, θ kontaktní úhel měřené kapaliny na
materiálu kapiláry) a tíhou kapaliny ve sloupci ρgh.
Pro povrchové napětí pak platí γ=ρgrh /2cosθ .
(obrázek z [4])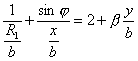 , v níž
, v níž  měření znázorňuje obrázek
z publikace [
měření znázorňuje obrázek
z publikace [ Padday [
Padday [
