Předlohou pro konstrukci měřicího bloku se stala aparatura, kterou popisuje Wu [l28].
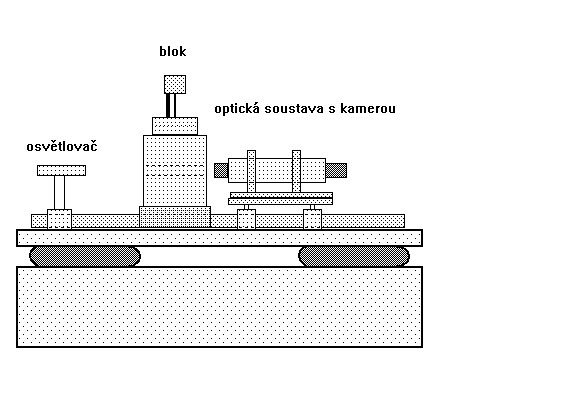
Úplná sestava měřicí aparatury odpovídá schématu na obrázku
o3.
Obrázek O3: Schéma aparatury na měření povrchového napětí.
Protože vibrace z prostředí bránily ustavení rovnovážných kapek vhodných k dalšímu zpracování, byla postupně zhotovena odrušená pracovní plocha: Na masivním podstavci vyplněném pískem, vrstvách polystyrenu a plsti a duších byla umístěna betonová deska. Na této desce byl umístěn asi 20 kg těžký litinový podstavec měřicí komory, opatřený výřezem pro optickou lavici, která s ním není v přímém kontaktu. Na optické lavici je umístěn zdroj světla
i snímací zařízení.Schema konstrukce vlastního bloku je na obrázkuo4.
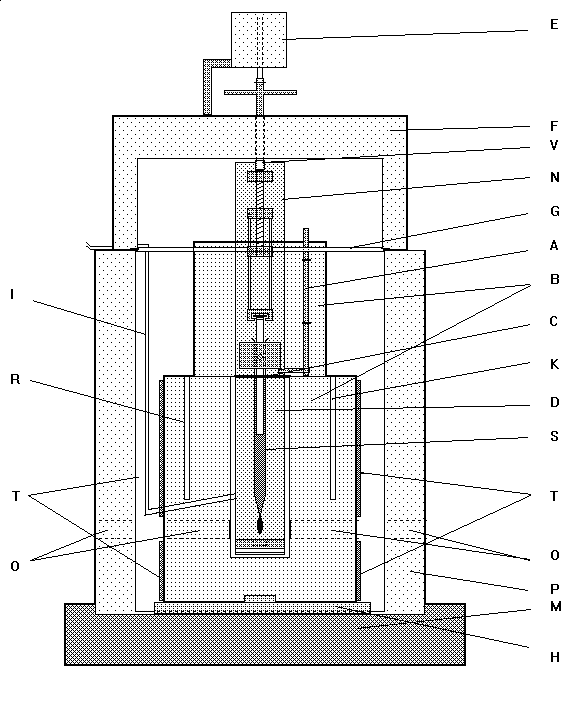
Obrázek O4: Komora pro měřený vzorek.
A: adjustační šroub, B: blok, C: plechové víčko šachty bloku, D: držák kyvety (misky), E: elektromotor, F: izolační víko pláště, G: teflonové víko, H: teflonová vložka, I: přívod inertního plynu, K: kontrolní teploměr, M: masivní podstavec, N: nosič injekční stříkačky, O: průzory, P: izolační plášť, R: řídicí teploměr, S: injekční stříkačka, T: topný plášť, V: výtlačný šroub
Blok (B) sestává z duralového válce o průměru asi 6 cm a délce kolem 10 cm. Při podélné ose válce je vyhloubena šachta na držák (D) s optickou kyvetou specolového typu, případně s kovovou miskou při měření povrchového napětí. Za tímto držákem se vsouvá nosič (N) s injekční stříkačkou (S), mající konec vytažen do kapiláry, tak, aby konec kapiláry byl uvnitř kyvety, popř. nad miskou. Na úrovni konce kapiláry jsou vedeny blokem kruhové otvory (O) ve směru kolmém na osu válce, v optické ose celé aparatury. Blok je vytápěn topným pláštěm (T) z odporového drátu, členěným na 5 sektorů a s celkovým maximálním výkonem 150 W. Výkon je regulován regulátorem teploty z produkce VD ČSAV na základě údajů řídicího platinového teploměru (R) umístěného v bloku. Ke kontrole teploty slouží druhý platinový teploměr (K). Celý blok je umístěn v izolačním plášti (P) naplněném křemelinou. Průzory v plášti i bloku v optické ose byly osazeny původně podložním sklem mikroskopu, později kvůli zkreslení a kontrastu nahrazeny průzorem z optického skla. Píst injekční stříkačky je ovládán pomocí šroubu (V), kterým může být otáčeno ručně nebo elektromotorem (E) majícím spínač na pohyblivém přívodu, což umožňuje spínání při současném pozorování kapky. Poloha konce kapiláry může být nastavena adjustačním šroubem (A) se zarážkou. Do vnitřní šachty je přiváděn inertní plyn (I) (při provedených měřeních dusík). Šachta je zakryta plechovým víčkem (C), jež je opatřeno otvorem pro stříkačku. Celý vnitřek pláště je kromě izolačního víka (F) opatřen teflonovým víčkem (G). Blok je zespodu izolován teflonovou vložkou (H) a z důvodu mechanické stability stojí na masivním litinovém podstavci (M).Kapka je osvětlována světlem z wolframové žárovky paralelizovaným spojnou čočkou. Zpočátku používaná zobrazovací soustava se skládala z objektivu Anaret 4,5/105 mm, vzdáleného ca. 10 cm od kapky, a objektivu Pentacon 1,8/50 mm. Vzdálenost mezi objektivy pro zvětšení 10x byla 0,5 m, mezi filmem a objektivem 0,15 m. Při vzdálenosti mezi objekti
vy 0,33 m bylo zvětšení asi 6 x. Protože se zvětšení ve druhém stupni ukázalo jalovým (nezvyšujícím rozlišovací schopnost), byl posléze druhý objektiv vyřazen a vzdálenost objektiv - film pak byla ca. 50, 70, 80 nebo 95 cm (zvětšení zhruba 5 - 10x). V daném uspořádání byla používána expoziční doba v rozmezí 1/125 až 1/1000 s při používaných filmech o citlivosti 19 - 21 ČSN.Tento obraz byl u měření prováděných mezi koncem roku 1991 a lednem 1993 snímán z negativu kamerou Panasonic při rozlišení 512x512 bodů v 256 jasových úrovních. Z obrazu byl určen obrys kapky prahováním, v případě nerovnoměrné expozice snímku byl obraz vyrovnáván početní simulací přisvětlování. Další zpracování je popsáno v oddíle i5.2.3 o zpracování výsledků.
Od ledna 1993 bylo snímání pr
ováděno přímo CCD kamerou Elvia OS-458 přes zařízení Matrox IP-8 s rozlišením 768x576 bodů při 256 jasových úrovních za použití objektivu Anaret 4,5/105 mm. Vzhledem k malé velikosti čipu kamery postačilo zvětšení 2-3x. Vysoká citlivost kamery si vyžádala výrazné snížení intenzity osvětlení kapky, čehož bylo dosaženo snížením napětí na žárovce a zařazením matnice mezi zdroj světla a kapku.Rozlišovací schopnost byla pomocí kontrolních obrazců VÚZORT stanovena 100 čar/mm. To odpovídá přesnosti měření rozměrů 0,3 až 0,5% a tím podle rovnice (r3-9) a tabulky t3.6 chybě 1,5 až 3,5% v určení povrchového napětí. Orientační test pomocí milimetrového papíru, který by odhalil zkreslení nad 1 až 2 %, neukázal takové zkreslení. K přesnému stanovení chyběly zvětšené sr
ovnávací obrazce.Pro měření je třeba vzorek zbavit plynů, protože bubliny v kapce nepříznivě ovlivňují výsledek měření [l1]. Vzorek polymeru (práškový nebo granulový) byl umístěn do injekční stříkačky (skleněná s kovovým pístem), ta umístěna do pece v poloze otvorem vzhůru. Pec byla naplněna dusíkem a zahřáta na teplotu ca. 30 K nad teplotu tání vzorku a po 1-4 hodinách evakuována. Aby se usnadnilo uvolňování bublin z tav
eniny, byl držák se vzorkem vystaven úderům mechanického zařízení. Po dalších 2 hodinách byla pec napuštěna dusíkem, stříkačka za horka vyjmuta a vytlačeny bubliny. Vzhledem k tomu, že příprava i měření zabíraly více hodin, nebyl vzorek přenášen do měřicí komory v teplém stavu nechával se vzorek vychladnout přes noc (po vytlačení bublin se umisťoval zpět do dusíkového prostředí) a měření pokračovalo až jiný den. Některé vzorky přes inertní prostředí po vytlačení žloutly, při vyšších teplotách i ve stříkačce; hodnoty z těchto teplot nejsou zpravidla již zahrnuty do uváděných výsledků.Držák se stříkačkou obsahující vzorek byl umístěn do bloku zpravidla za pokojové teploty. Po zavedení dusíku do prostoru měření bylo spuštěno zahřívání. Polymer se vytlačoval až po dosažení teploty měření a asi půlhodinovém ustálení. První jedna až dvě kapky nebyly snímány pro vyhodnocování. Kapky měly být snímány do ustálení rovnovážného tvaru. Vzhledem k tomu, že nikdy nebyl zcela zastaven tok taveniny z k
apiláry, bylo očekáváno, že se tvar kapky a tím vypočtené povrchové napětí bude s časem blížit určité hodnotě, a při počátku odtrhávání se opět odchýlí. Za hodnoty pro další zpracování by pak byly brány hodnoty v tomto stabilním úseku, přičemž by byly vyloučeny kapky tvaru zjevně nepravidelného. Celá doba od vytlačení kapky do jejího samovolného utržení, popř. záměrného odkápnutí, se pohybovala od několika minut při horní hranici teplotního intervalu k deseti hodinám u teplot blízko nad bodem tání. Počet kapek vyhodnocovaných při jedné teplotě byl nejméně tři, při vyšších teplotách, kdy byla měření rychlejší, bylo vyhodnocováno až kolem dvaceti kapek.Pro účely této práce byly hustoty měřeny v dilatometrech tvaru U s odnímatelnou baněčkou
, spojenou s vlastní trubicí zábrusem (obrázek o5).Objem kapaliny dosahující v dilatometru k jednotlivým ryskám (Vd
) byl předem kalibrován rtutí, při vlastním měření byl dilatometr hmotnosti md naplněn zváženým polymerem o hmotnosti mp, po doplnění rtutí určena celková hmotnost mf (= md+mp+ mHg ). Objem polymeru byl pak určován jako rozdíl objemu celé náplně a objemu rtuti, takže hustota polymeru mohla být počítána pomocí vzorce:
= mp/Vp= mp/[ Vd- (mf-md-mp)/Hg] (R3-1)Pro hustotu rtuti byl
a používána rovnice podle referenčních hodnot IUPAC [l64]:
Hg= [-5,610-7(T-0°C)3+ 3,810-4(T-0°C)2- 2,468(T-0°C) + 13595,1] kgm-3 (R3-2)Kalibrace dilatometrů byla prováděna při pokojové teplotě, podle původního záměru měla být prováděna i korekce na změnu objemu dilatometru s teplotou, ta však byla menší než chyba měření.
Dilatometry se silnější kalibrovanou trubicí o vnitřním průměru 3,6 mm umožňovaly vzhledem k rozsahu použitelných vah přesnost určení objemu pouze kolem 1%, proto byla většina měření provedena na dilatometrech s průměrem kapiláry 2 mm, které umožnily přesnost měření kolem 0,3%.
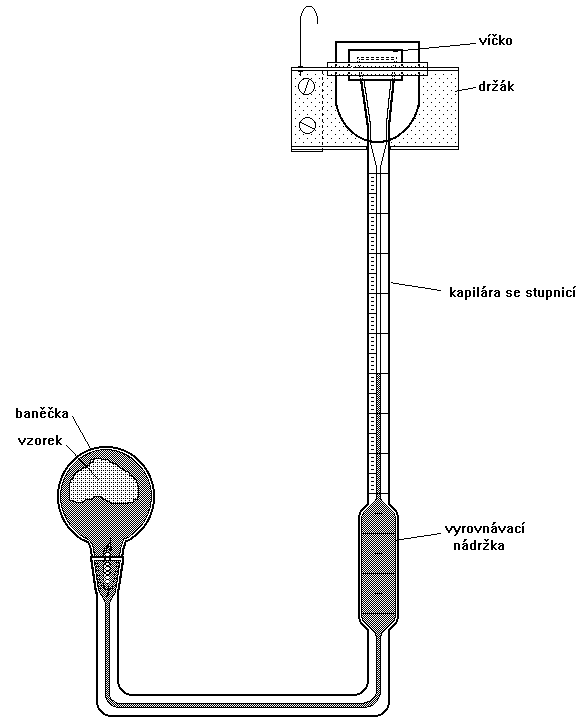
Obrázek O5: Dilatometr
Zkreslujícím činitelem je velký odpar rtuti při teplotách nad 200 C. Rovněž optické odečítání hladiny rtuti zanášelo do výsledků nepřesnosti, poněvadž si vyžadovalo povytažení kapiláry z lázně. To zejména při vyšších teplotách měření znepřesnilo a znejistilo naměřené hodnoty. K vyloučení tohoto vlivu bylo sice sestrojeno zařízení na indikaci hladiny rtuti pomocí elektrického konta
ktu, nepodařilo se však dosáhnout spolehlivého spínání za vyšších teplot. Proto byly výsledky prezentované v této práci získány bez jeho použití.Při dilatometrickém měření hustoty se vycházelo buď ze vzorku práškového či granulového, nebo z vlákna vytlačeného při teplotě asi 20 K nad teplotou tání. Odváženým vzorkem byla naplněna baněčka zváženého a zkalibrovaného dilatometru, dilatometr ponechán několik desítek minut pod vakuem, opět zvážen a pod vakuem naplněn rtutí. U práškových vzorků se ukázala nutnos
t před plněním rtutí vzorek přetavit pod vakuem, aby nebyly výsledky zkreslovány bublinami. Toto přetavení se dělo v baněčce dilatometru ponořené do solné lázně o teplotě asi 210 C až 220 C u polypropylenů, 180 C u polyethylenů.Po zvážení byl plný dilatometr umístěn do lázně (silikonový olej do 200-250 C, solná směs pro 180-300 C) a temperován na teplotách s intervalem 10 K v oblasti rovnoměrné roztažnosti (20-30 K při teplotách nad 220 C), 1 K v oblasti přechodů. Hladina dilatometru byla odečítána nejprve
asi 5-10 min po dosažení nastavené teploty, podruhé asi po 30 minutách, a pokud se tyto údaje lišily, po dalších 30 minutách nebo i delším časovém intervalu; při teplotách dostatečně nad bodem tání bylo odečítáno pouze jednou po asi 10 min, protože se jednak ukazovalo poměrně rychlé ustálení objemu na stálé hodnotě, jednak se při vyšších teplotách rychle odpařovala rtuť a tvořila na stěnách kapiláry zrcátko, což znesnadňovalo odečet a zkreslovalo výsledky měření. Vzhledem k tomu, že bylo měřeno v rozsahu od pokojových teplot, byly jako vedlejší údaj získány i teploty fázových přechodů (tání).Jako ověřovací vzorek pro všechna měření byl použit poly(oxydimethylsilandiyl) značky Aldrich, katalogového čísla 18,183-8. Katalog firmy neobsahuje jeho bližší charakteristiku. Běžně užívaný, ale IUPAC nedoporučený [l104], název této látky je polydimethylsiloxan a zkratka PDMS. Hmotnostně průměrná molekulová hmotnost byla zjištěna 137000 [l105].
Dále měřené vzorky byly vybírány s ohledem na systémy polymerních směsí zkoumané dr. Fortelným. Jedná se technické polymery - aditivované polyethyleny, aditivované a surové polypropyleny a jeden vzorek polystyrenu.
Byly použity technické lineární polyethyleny s obchodním názvem Liten, vyráběné v CHZ Litvínov fluidní polymerací ethylenu. Jsou charakterizovány indexem toku v gramech za 10 minut při zatížení 21,19 N a teplotě 190 °C (dále značen ITv) a poměrem indexů toku při zatíženích 212 N a 21,
2 N (dále MFRv). Krystalinita je udávána 60-80%. Podle výrobce klesá hustota s rostoucí molární hmotností [l106].Dále nám byly Výzkumným ústavem makromolekulární chemie v Brně poskytnuty [l107] údaje o indexech toku při zatížení 23,05 N (IT) a poměru indexu toků při zatíženích 230,5 N a 23,05 N (MFR) s tím, že pro hmotnostně průměrnou molární hmotnost
log(![]() ) = 4,798 - 0,299
) = 4,798 - 0,299
log(I) = - 1,158 - 0,0719
log(IT) + 1,248log(MFR) (R3-4)Podle těchto rovnic byly z udaných hodnot IT a MFR počítány molární hmotnosti.
Údaje o vzorcích podle katalogu shrnuje tabulka t3.1. Hodnoty i
ndexů toku podle obou zdrojů a z nich vypočítané molární hmotnosti uvádí spolu s molárními hmotnostmi z jiných zdrojů (případně specifikovaných v dalším textu) tabulka t3.2.Tabulka T3.1: Vlastnosti polyethylenů Liten podle katalogu
|
druh |
hustota |
bod tání |
aditivace |
určení |
|
|
Litenu |
kg m |
°C |
|||
|
BB 29 |
952-3 |
kopola |
UV,základní |
vyfukovací |
|
|
MB 57 |
955 |
126-130 |
kopola |
základní |
vstřikovací |
|
MB 62 |
961 |
130-133 |
homop |
základní |
vstřikovací |
|
MB 82 |
962 |
120-131 |
homop |
základní |
vstřikovací |
a
: s 1-butenemTabulka T3.2: Ind
exy toku Litenů a z nich získané molární hmotnosti|
druh |
katalog |
VÚMCH |
z ind. toku |
měřené ÚMCH |
||||
|
Litenu |
IT |
MFR |
IT |
MFR |
M |
M |
M |
M |
|
BB 29 |
0,12 |
? |
0,15 |
90 |
31000 |
270000 |
||
|
MB 57 |
4 |
45 |
4 |
30 |
47000 |
81000 |
||
|
MB 62 |
6 |
45 |
11000 |
88000 |
||||
|
MB 82 |
15 |
45 |
14 |
30 |
35000 |
56000 |
||
Molární hmotnost Litenu MB62 byla měřena kolektivem pracovníků ÚMCH ČSAV [l85], [l109]. Rovněž jsou změřeny hodnoty Litenu FB29, podobného Litenu BB29. Jeho molární hmotnost je -[l109]
Měřeny byly technické polypropyleny vyráběné v CHZ Litvínov. Polymerují se v rozpouštědle. Obsahují 95-97% isotaktického podílu, krystalinita činí asi 60 %, hustota kolem 900
kgm-3, teplota skelného přechodu -10 °C, teplota tání 160 až 168 °C, c při 20 C 0,84 kJ/(kg K), při 100 °C 2,5 kJ/(kg K). Indexy toku jsou udávány v g/10 min při teplotě 230 C a zatížení 21,2 N. Podle výrobce klesá hustota s rostoucí molární hmotností [l106]. Pro vztah molární hmotnosti a indexu toku poskytl Hudec [l108] rovnicilog (IT) = 18,49 - 3,23
log(Údaje o vzorcích podle katalogu shrnuje tabulka t3.3.
Hodnoty indexů toku a z nich podle rovnice (r3-5) vypočítané molární hmotnosti uvádí tabulka t3.4 spolu s molárními hmotnostmi změřenými ve VÚMCH Brno gelovou permeační chromatografií u Mostenu 53692 [l111] a Mostenu PH6 [l108].TabulkaT3.3: Vlastnosti p
olypropylenů Mosten dle katalogu|
druh |
hustota |
bod tání |
aditivace |
určení |
|
|
Mostenu |
kg m-30 |
°C |
|||
|
52422 |
9 0 7 |
homop |
tepelná |
vstřikovací |
|
|
52522 |
9 0 7 |
160-163 |
homop |
tepelná |
vstřikovací |
|
53692 |
9 1 0 |
130-133 |
homop |
speciální |
foliový |
Tabulka T3.4: Indexy tok
u Mostenů a z nich získané molární hmotnosti|
druh |
katalog |
VÚMCH |
z ind. toku |
změřené |
|
|
Mostenu |
IT |
IT |
M |
M |
M |
|
Mosten 52422 |
3,2 |
3 |
370000 |
||
|
Mosten 52522 |
4,5 |
5 |
333000 |
||
|
Mosten 53692 |
|
8 |
280000 |
38000 |
350000 |
|
Mosten PH1 |
|
do 0,5 |
650000 |
||
|
Mosten PH4 |
|
2 - 4 |
350000 |
||
|
Mosten PH6 |
|
6 - 9 |
300000 |
55000 |
300000 |
Krasten 127 je technický polystyren vyráběný v Kaučuku Kralupy. Podle katalogu [l106] je to perličkový polystyren vyráběný suspensní polymerací čistého styrenu; základní vstřikovací typ. Hustota 1050
kgm-3, index toku 15-20 g/10 min při 200 °C a zatížení 5 kg. Teplota zeskelnění ca.85 °C. Bez přísad.
V většině teorií týkajících se polymerů vystupuje počet segmentů v polymerním řetězci, který může být v různých teoriích vymezen různě. Nelze-li tento počet zjistit jinak, je třeba udělat vlastní vymezení segmentu. Z nabízejících se možností zde budou vyčísleny délky segmentů pro tři definice segmentu: jako mer (M), jako část molekuly připadající na atom hlavního řetězce (H) nebo jako část molekuly připadající na jeden řetězotvotný atom (C, příp.Si,O) (C). V závorce uvedené značení je dále už
íváno jako krátký odkaz na jednotlivé volby.TabulkaT3.5: Některé volby segmentu pro polymery
|
relativní molekulová hmotnost |
|||
|
látka |
meru |
na at.hl.řet. |
na C (Si,O) |
|
PDMS |
74 |
37 |
18,5 |
|
PE |
28 |
14 |
14 |
|
PP |
42 |
21 |
14 |
|
PS |
104 |
52 |
13 |
|
označ |
M |
H |
C |
Pro použité výpočty je rozhodující početně průměrná molární hmotnost. Proto byly na ně převedeny hmotnostně průměrné molární hmotnosti látek, u nichž nebyl početní střed znám, a to s předpokladem stejné polydispersity jako u vzorků, kde byly známy oba středy.
V oddíle d2.7 byly uvedeny způsoby zpracování výsledků měření povrchového napětí. Následující odstavce se zabývají tím, jak se do konečných výsledků promítá experimentální chyba
Pro chybu určení veličiny, jež je funkcí veličin
qi nezávisle měřených s chybami qi platí [l67]: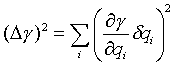 (R3-6)
(R3-6)
(
)2=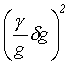 +
+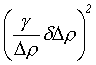 +
+ +
+kde 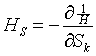
Relativní chyba je vyjádřena [l67] rovnicí:
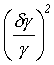 =
=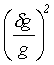 +
+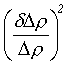 +
+![]() (2+H
(2+H
Za předpokladu, že měření všech rozměrů vykazuje stejnou chybu
d, lze rovnici(r3-8) upravit do tvaru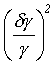 =
= 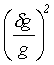 +
+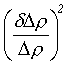 +Pd
+Pd![]()
![]() (R3-9)
(R3-9)
kde činitel příspěvku relativní chyby měření rozměrů
Pd jeP
d= 4+4HHsSk + (HHsSk)2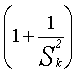 (R3-10)
(R3-10)
Hodnoty činitele
P pro řez v 1,0 násobku maximálního průměru (tj. k=1,0) jsou vypsány v tabulce t3.6.Tabulka T3.6: Hodnoty činitele příspěvku relativní chyby měření rozměrů
P pro vybranou rovinu s koeficientem 1,0:|
S |
0 |
0,30 |
0,40 |
0,50 |
0,60 |
0,68 |
0,70 |
0,80 |
0,90 |
0,96 |
1,00 |
|
P |
∞ |
99,5 |
65,3 |
49,4 |
40,7 |
36,4 |
35,5 |
32,4 |
30,9 |
30,6 |
30,7 |
Rovnice (r3-9) spolu s tabulkou t3.6 ukazují, že citlivost celkové chyby určení povrchového napětí k chybě určení rozměrů je (v 2.mocnině) 30 až 50 krát větší než vůči chybě určení ostatních veličin.
Vyhodnocován zpravidla bývá obraz kapky ve zvětšeném měřítku. Upravíme-li rovnici (r2-139) tak, že vyjádříme velikost
d pomocí velikosti obrazu D a zvětšení obrazu K :H= (R3-11)
(R3-11)
přechází rovnice (r3-9) na obdobný tvar:
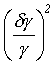 =
= 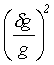 +
+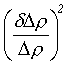 +
+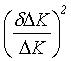 + P
+ P
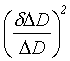 (R3-12)
(R3-12)
která ukazuje, že na chybu převodu do správného měřítka je výsledná hodnota méně citlivá než vůči chybě určení parametrů tvaru.
Roe [l72] při svém rozboru chyb ještě uvažuje dvě složky chyby měření
d : chybu určení vybrané roviny a vlastní chybu s měření. Kvadrát chyby plynoucí z určení 1/H podle něj odpovídá: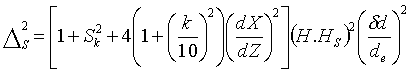 (R3-13)
(R3-13)
V rozdílu mezi hodnotami povrchového napětí vypočítanými z rozměrů v jednotlivých
vybraných rovinách, se mohou promítnout zejména následující faktory:1. Chyby vzniklé při zobrazování kapky a proměřování obrazu:
a, Chyba určení maximálního průměru kapky
b, Chyba určení rozměru kapky v jednotlivých vybraných rovinách
2. Odchylky skutečného tvaru kapky od tvaru popsaného Bashforthovou - Adamsovou rovnicí (r2-135) zapříčiněné nedokonalým splněním podmínek její platnosti, především mechanickou nerovnováhou. K odhadnutí, zda chyba dle bodu 1a působí, že se naměřená hodnota povrchového napětí
posouvá systematicky podle vybrané roviny užité k vyhodnocování, byl proveden následující test: Za základ byla vzata teoretická křivka, vypočtená pro parametr β= 0,25. Tato křivka byla vyhodnocována stejným způsobem jako měřené křivky s tím, že místo maximálního průměru byly dosazovány různé hodnoty lišící se oběma směry od skutečné hodnoty. Ostatní souřadnice křivky zůstaly nezměněny s tím, že byly zpracovávány s přesností na 3 platné číslice, což je praktická přesnost měření rozměrů kapky. Bylo sledováno, zda nastává závislost povrchového napětí na vybrané rovině. Ostatní modelové parametry byly zvoleny tak, aby se blížily hodnotám v reálných systémech. Výsledky shrnuje tabulka t3.7.Pro maximální průměr kapky 2,5573 mm při přesnosti dosazování průměrů ve vybraných rovinách na 4 platná místa byla průměrná vypočtená hodnota povrchového napětí (58,37±0,01) mN m
-1 a směrnice dγ /dk -0,08 mN m-1.Uvedené výsledky ukazují, že chyby v určení maximálního průměru kapky se poměrně výrazně projevují v závislosti získaných hodnot na vybrané rovině (při matrici 512 x 512 bodů, která odpovídá dosažené rozlišovací schopnosti, se chyba určení o 2 body projeví rozptylem téměř 5% a posunem průměru o 10% od správné hodnoty).
Tabulka T3.7: Povrchová napětí zpětně získaná z teoretické křivky v závislosti na zkreslení hodnoty maximálního průměru:
|
Povrchové napětí/(mN m -1 ) |
|||||
|
max. průměr [m m] |
2,439 |
2,5365 |
2,557 |
2,561 |
2,683 |
|
k = 0,8 |
25,14 |
49,37 |
58,16 |
60,03 |
381,8 |
|
k = 0,9 |
32,04 |
52,16 |
58,27 |
59,67 |
136,7 |
|
k = 1,0 |
37,01 |
53,79 |
58,40 |
59,23 |
98,0 |
|
k = 1,1 |
41,06 |
54,91 |
58,42 |
58,97 |
82,9 |
|
k = 1,2 |
44,36 |
55,72 |
58,40 |
58,84 |
74,9 |
|
průměr |
35,9 |
53,2 |
58,33 |
59,35 |
155 |
|
odchylka |
6,8 |
2,25 |
0,10 |
0,45 |
115 |
|
d γ/ d k |
47,5 |
15,4 |
0,63 |
-3,3 |
-668 |
Modelové parametry:
|
=0,25 |
1/H=0,90962 |
|
b=1,2195 mm |
=58,36mNm-1 |
|
g=9,8077 m s-2 |
max.pr ůměr=2,5573mm |
|
=1000kgm-3 |
Chyby uvedené pod bodem 1b lze pokládat za náhodné. Chyby způsobené skutečnou deformací kapky představují nejdůležitější faktor ovlivňující použitelnost metody. Projevují se rozptylem hodnot naměřeného povrchového napětí a působí zpravidla i posun určené střední hodnoty povrchového napětí. Z hlediska závislosti vypočtených hodnot povrchového napětí na použité vybrané rovině a velikosti jeho rozptylu lze uvažovat několik kombinací.
Je-li rozptyl větší, než by přicházelo v úvahu, kdyby byl způsoben jen chybou měření rozměrů obrazu, a není-li zjištěna závislost vypočtených povrchových napětí na rovině měření, jedná se zřejmě o skutečnou deformaci kapek, a to pravděpodobně místními poruchami v jejím přibližně r
ovnovážném tvaru. Průměrná hodnota se pravděpodobně liší od skutečné hodnoty povrchového napětí. Nachází-li se kapka v nerovnovážném, ale relativně ustáleném stavu s válcovou symetrií, kterým prochází při ustavování rovnovážného stavu po vytlačení v prostředí bez rušivých vlivů, projevuje se závislost zjištěné hodnoty povrchového napětí na vybrané rovině podobným způsobem, jako efekt uvedený pod bodem 1a. Viskosní kapaliny zaujímají bezprostředně po vytlačení z kapiláry tvar vlákna, ze kterého zvolna přecházejí do tvaru řídícího se Bashforthovou - Adamsovou rovnicí (r2-135). Na počátku se všechny poměry Sk blíží jedné. Tomu odpovídá zjištění povrchového napětí menšího než je ve skutečnosti, obvykle s menšími hodnotami získanými z rovin vzdálenějších od vrcholu kapky. Pokud kapka ztrácí rovnováhu a směřuje k odkápnutí, vytváří se úzký krček, oproti rovnovážnému tvaru se zmenšují průměry řezů ve vybrané rovině, a to výrazněji ve větší vzdálenosti od vrcholu. Tomu odpovídá zjištění povrchového napětí většího než je ve skutečnosti, obvykle s největšími hodnotami získanými z rovin vzdálenějších vrcholu kapky.Jak se uvedené příčiny projevují na závislosti zjištěných povrchových napětí na relativní vzdálenosti vybrané roviny od vrcholu kapky a na odchylce naměřených hodnot povrchového napětí od hodnot skutečných shrnuje tabulka t3.8.
TabulkaT3.8: Projev rušivých vlivů při měření povrchového napětí
|
příčina |
γ exp-γskut |
dγ/d k |
|
nadhodnocení de |
kladná |
záporná |
|
podhodnocení de |
záporná |
kladná |
|
kapka před ustálením |
záporná |
záporná |
|
odkapávající kapka |
kladná |
kladná |
Součástí příprav vyhodnocování výsledků byla i tvorba programů. Jednalo se především o program na integraci Bashforth - Adamsovy rovnice (r2-137) a určení parametrů
de /b a de /b pro jednotlivé vybrané roviny. Integrace končí dosažením krčku (minima průřezu kapky); na rozdíl od Fordhamových tabulek tedy tabulka neobsahuje hodnoty S pro případy, kdy vybraná rovina leží nad krčkem. Moduly tohoto programu byly použity i v programech majících určit regresními metodami β a b z experimentálních bodů např. Rotenbergovým [l69] postupem.Výsledné tabulky byly uvedeny v dřívější práci [l112]. Od Staufferových tabulek se výsledky liší více pro malé hodnoty parametru beta a pro počáteční části křivek.
Výše byla zmíněna Misakova rovnice (r2-142) pro náhradu tabulek závislosti 1/
H na S. Pokusil jsem se nahradit rovnicemi závislost pro všechny roviny. Rovnici tvaru (r2-142) nelze s uspokojivou přesností použít pro ostatní roviny. Použije-li se jako výchozí aproximace místo rovnice (r2-141) rovnice tvaruln(1/H) = ln (k
e)+ kexln(S)2 + kepln(S) , (R3-14)získáme místo (r2-142) rovnici
1/H = ke
S(kexln(S)+kep)+ k3S3 + k2S2 + k1S + k0 (R3-15)která se zdála poskytovat neju
spokojivější výsledky z vyzkoušených možností [l113].Tato rovnice byla uplatněna na 1/
H a S získaná integrací Runge-Kuttovou metodou 4. řádu s krokem 0,00025 pro síť hodnot lišících se o 0,0005. Velikost intervalů pro proložení rovnicí (r3-15) byla volena tak, aby relativní velikost maximální odchylky 1/H v intervalu pokud možno nepřesáhla 10-4; v okrajových intervalech byla tato odchylka někdy větší. Získané hodnoty koeficientů jsou uvedeny v tabulce t3.9.Tabulka T3.9: Koeficienty rovnice (r3-15)
Pro ře
z v 0,8 násobku d :|
Interval S |
k e |
kex |
kep |
k 3 |
k 2 |
k 1 |
k 0 |
|
|
min |
max |
|||||||
|
0.82 |
0.83 |
1791452.8 |
533.85850 |
170.55837 |
-81676.15812 |
202187.89690 |
-166836.27680 |
45888.22973 |
|
0.83 |
0.84 |
189.07578 |
272.52455 |
72.730022 |
-19963.60152 |
50019.79936 |
-41775.38186 |
11629.85610 |
|
0.84 |
0.85 |
7.1549709 |
165.45945 |
35.285687 |
-6944.66848 |
17609.43832 |
-14883.84379 |
4193.34232 |
|
0.85 |
0.87 |
1.1496269 |
95.066407 |
12.600013 |
-2158.91585 |
5571.60176 |
-4792.82331 |
1374.26272 |
|
0.87 |
0.895 |
0.47873040 |
50.357240 |
0.089787883 |
-567.76534 |
1503.51828 |
-1327.11835 |
390.45562 |
|
0.895 |
0.93 |
0.35255000 |
25.498893 |
-5.4176608 |
-165.99710 |
454.58851 |
-414.93772 |
126.23908 |
|
0.93 |
0.97 |
0.32002037 |
6.8474560 |
-8.0901766 |
-102.84970 |
293.25377 |
-278.69176 |
88.27639 |
|
0.97 |
0.99 |
0.30845061 |
-32.343947 |
-10.455428 |
-475.69091 |
1398.86173 |
-1371.17931 |
448.00538 |
|
0.99 |
0.999 |
0.30110729 |
-333.50440 |
-15.711260 |
-11334.69334 |
33822.93507 |
-33642.61426 |
11154.37157 |
Pro řez v 0,9 násobku
d :|
Interval S |
ke |
kex |
kep |
k3 |
k2 |
k 1 |
k0 |
|
|
min |
max |
|||||||
|
0.635 |
0.645 |
58249804 |
119.64583 |
89.483167 |
-28072.11478 |
53918.28040 |
-34519.94034 |
7366.77050 |
|
0.645 |
0.66 |
5100.2910 |
70.920100 |
46.811007 |
-9051.10879 |
17726.62108 |
-11572.21470 |
2518.10214 |
|
0.66 |
0.685 |
19.518159 |
38.509198 |
19.951285 |
-2338.00251 |
4719.64936 |
-3175.58038 |
712.17229 |
|
0.685 |
0.72 |
1.3823760 |
20.055606 |
5.9746092 |
-522.67397 |
1102.26575 |
-774.75596 |
181.49582 |
|
0.72 |
0.77 |
0.49074291 |
10.484929 |
-0.31885445 |
-111.99730 |
250.54286 |
-186.78287 |
46.40581 |
|
0.77 |
0.84 |
0.34607161 |
5.4063548 |
-2.9788620 |
-24.21100 |
58.53312 |
-47.15244 |
12.65668 |
|
0.84 |
0.93 |
0.31342828 |
2.1140055 |
-4.1151543 |
-9.16969 |
24.37544 |
-21.58758 |
6.36954 |
|
0.93 |
0.98 |
0.30397966 |
-3.6334200 |
-4.9395699 |
-29.80626 |
85.43510 |
-81.61766 |
25.98669 |
|
0.98 |
0.997 |
0.30007321 |
-34.095653 |
-6.1531194 |
-434.11439 |
1287.65238 |
-1273.10762 |
419.56923 |
Pro řez v 1,0 násobku
d :|
Interval S |
ke |
kex |
kep |
k3 |
k2 |
k 1 |
k0 |
|
|
min |
max |
|||||||
|
0.17 |
0.31 |
0.31081678 |
-0.086278355 |
-2.7023254 |
-13.95071 |
10.30398 |
-2.49619 |
0.19805 |
|
0.30 |
0.45 |
0.30636442 |
-0.094871613 |
-2.7246428 |
0.38766 |
-0.44128 |
0.16613 |
-0.02068 |
|
0.45 |
0.68 |
0.31156188 |
-0.063734909 |
-2.6789763 |
0.41537 |
-0.71168 |
0.40321 |
-0.07551 |
|
0.68 |
0.90 |
0.31195754 |
-0.092720991 |
-2.6863859 |
-0.44813 |
1.06637 |
-0.84260 |
0.22106 |
|
0.90 |
0.983 |
0.30712046 |
-1.5619311 |
-2.9809169 |
-5.74538 |
16.23781 |
-15.29128 |
4.79808 |
Pro řez v 1,1 násobku
d :|
Interval S |
k e |
k ex |
k ep |
k 3 |
k 2 |
k 1 |
k 0 |
|
|
min |
max |
|||||||
|
0.06 |
0.08 |
1.6030433 |
0.043380701 |
-0.15208454 |
-1341.32950 |
282.27311 |
-19.71010 |
0.45664 |
|
0.08 |
0.13 |
0.85491410 |
-0.056761738 |
-0.65372414 |
-160.97221 |
50.59168 |
-5.23625 |
0.17842 |
|
0.13 |
0.20 |
0.57401485 |
-0.15265815 |
-1.0443069 |
-42.79943 |
21.22139 |
-3.47357 |
0.18765 |
|
0.20 |
0.30 |
0.41622542 |
-0.27871823 |
-1.4464670 |
-14.08741 |
10.58863 |
-2.63159 |
0.21621 |
|
0.30 |
0.44 |
0.33587066 |
-0.42674255 |
-1.8022482 |
-3.22540 |
3.58964 |
-1.32194 |
0.16106 |
|
0.44 |
0.75 |
0.31504207 |
-0.51197565 |
-1.9499037 |
0.07609 |
-0.13681 |
0.08090 |
-0.01572 |
|
0.75 |
0.953 |
0.31658938 |
-0.49808609 |
-1.9290368 |
-0.24018 |
0.61450 |
-0.52258 |
0.14771 |
Pro řez v 1,2 násobku
d :|
Interval S |
ke |
kex |
kep |
k3 |
k2 |
k 1 |
k 0 |
|
|
min |
max |
|||||||
|
0.10 |
0.12 |
103.56308 |
1.2019976 |
4.4869062 |
-6625.95443 |
2292.46751 |
-264.28560 |
10.15218 |
|
0.12 |
0.14 |
2.1585254 |
0.34129627 |
0.83653215 |
-742.15388 |
289.52312 |
-37.59979 |
1.62555 |
|
0.14 |
0.19 |
0.65654048 |
0.031877859 |
-0.37693028 |
-66.92134 |
33.18430 |
-5.45788 |
0.29773 |
|
0.19 |
0.27 |
0.45076908 |
-0.10378254 |
-0.82836350 |
-10.66154 |
7.36263 |
-1.68453 |
0.12768 |
|
0.27 |
0.40 |
0.37085833 |
-0.21965481 |
-1.1287016 |
-2.87493 |
2.88810 |
-0.95966 |
0.10546 |
|
0.40 |
0.55 |
0.33605594 |
-0.33317467 |
-1.3397591 |
-0.70394 |
1.00402 |
-0.47492 |
0.07450 |
|
0.55 |
0.902 |
0.32790337 |
-0.39597877 |
-1.4180887 |
0.00490 |
-0.01070 |
0.00769 |
-0.00182 |
Maximální odchylky hodnoty interpolační funkce (r3-15) od integrací získané hodnoty 1/
H shrnuje tabulka t3.10.Tabulka T3.10: Maximální odchylky interpolační funkce
|
Rovina řezu |
Absolut ní odchylka |
Relativ ní odchylka |
||
|
hodnota |
pro Sk |
hodnota |
pro Sk |
|
|
0.8 |
0.00016 |
0.999 |
0.0005 |
0.999 |
|
0.8 (0.83<S<0.99) |
-0.00017 |
0.85 |
-0.00009 |
0.85 |
|
0.9 |
-0.0004 |
0.66 |
-0.0001 |
0.66 |
|
1.0 |
-0.0019 |
0.17 |
0.00006 |
0.45 |
|
1.1 |
-0.00026 |
0.08 |
-0.0001 |
0.30 |
|
1.2 |
-0.00012 |
0.14 |
-0.00008 |
0.14 |
Uvedené maximální odchylky nastávají zpravidla na rozhra
ní úseků a patří koeficientům pro úsek bližší hodnotám 0,9 až 0,95 (tj. nastávají na konci úseku vzdálenějším od těchto hodnot).Z obrázku kapky je určen její obrys. Za obrys byla brána posloupnost vzájemně sousedících bodů patřících do objektu a sousedících s body do objektu nepatřícími [l89]. Bod patřící do objektu je takový, jehož jas se nachází v určitém rozmezí. Používané způsoby určení obrysu byly zmíněny v odstavci i2.7.4. Při nastavení prahové hodnoty se vycházelo
zhruba z průměru mezi jasem bodu kapky poblíž povrchu a bodu pozadí poblíž kapky, později z průměru mezi vrcholky histogramu jasů; hodnota byla v případě potřeby interaktivně upravována tak, aby se vyloučily případné poruchy obrysu. Výsledkem tohoto kroku byl řetěz řádově 1000 bodů obrysu vyjádřených celočíselnými souřadnicemi. Pomocným kritériem pro odlišení kapky od ostatních předmětů (skvrn) v obraze se stal počet bodů obrysu kapky.V době používání rozpracovaného systému nám byl poskytnut program Račinského [l90], který určuje hranu z maximálního gradientu jasu obrazu, což umožňuje značné zpřesnění. Na druhou stranu tento program pracuje s hranicí definovanou pouze dvojicí bodů na každé řádce obrazovky, což vede k znepřesnění určení vrcholu kapky, ke kt
erému sice používá gradientu, ale pouze z jednoho prakticky náhodného řezu. V této práci byla příslušná procedura z jeho programu upravena a použita k zpřesnění obrysu získáného podle předešlého odstavce. Obrys byl rozdělen na intervaly např. po 5 bodech. Vzájemná poloha krajních bodů intervalu byla považována za směr hrany. Pokud byly tyto body příliš blízko u sebe (do dvojnásobku rozteče pixelů), bylo to považováno za známku místní poruchy a v tomto bodě nebyl další výpočet proveden, v opačném případě byl určen maximální gradient v jednom z 8 základních směrů nejbližším kolmici k hraně, v řezu procházejícím prostředním bodem skupiny. Na rozdíl od Račinského nebylo pracováno s absolutními hodnotami gradientu, které jsou snáze ovlivnitelné náhodnou chybou.Tí
mto postupem však nebyla zpracována data polymerů měřených před úpravou programu, protože se po zpracování původní datové soubory likvidují, archivují se pouze obrysy kapek a kalibračních těles.Výstupem tohoto kroku zpracování jsou tedy jednak soubor asi
1000 celočíselných bodů, jednak soubor asi 200 bodů zpřesněných. Další zpracování obou souborů nedávalo vzájemně výrazně odlišné výsledky, pokud nebyly směšovány kalibrace obou typů zpracování. Ve druhém kroku zpracování se vyhodnocuje geometrie kapek: pomocí obrysů kalibračních těles se převádějí obrysy kapek do skutečných rozměrů a počítají se parametry 1/H a de , popřípadě β a b (r2-136 , r2-139).Tento krok byl v této práci prováděn programem, který určí maximální průměr
de a průměry ve vybraných rovinách ds a z nich pomocí automatického prohledávání tabulek S - 1/H nebo náhradních rovnic počítá hodnoty 1/H, popřípadě i β a b. Program může optimalizovat výsledek rotací do polohy s nejmenším rozptylem výsledků poskytovaných jednotlivými vybranými rovinami, případně vyhodnocovat samostatně levou a pravou polovinu profilu; toto vyhodnocování polovin profilu však bylo posléze zavrženo jako náchylnější k chybám.Programy počítající regresními metodami, a tedy fakticky využívající více bodů, a tím odolnější vůči chybám, nebyly na našem pracovišti dosud odladěny tak, aby konvergovaly dostatečně blízko ke správným výsledkům. Výjimkou je proložení experimentálních bodů obrysu kapky polynomy, jejichž prostřednictvím byly vyhodnocovány průměry rovníku a vybraných rovin; k tomu byly použity postupy z programu Račinského [l90]. Třetím krokem zpracování je kombinace geometrických parametrů kapky 1/
H, de , β a b s údaji o hustotě polymeru a fyzikálních podmínkách měření, které poskytnou rovnicí (r2-139) povrchové, popř. mezifázové napětí. Tíhové zrychlení určeno s ohledem na zeměpisnou šířku, nepřihlíží se k nadmořské výšce (v našich zeměpisných šířkách se rozdíl 1 km jak v nadmořské výšce, tak ve vzdálenosti od rovníku projeví asi na 5.platném místě) a k lokálním anomáliím.Postupem času byly všechny kroky zpracování zahrnuty do snímacího programu, určení obrysu a jeho tvaru však jen v nejjednodušší podobě. Výsledkem bylo, že byly známy orientační hodnoty povrchového napětí pro právě zobrazenou kapku i jeho pohyb. Jako kritérium pro ustálenost výsledků pak bylo bráno, zda relativní pohyb povrchového napětí za danou dobu přesáhl kritickou hodnotu.
Přílohou práce jsou výpisy některých programů sestavených pro snímání dat a vyhodnocení experimentu a další výpočty. Vlastní čtení obrazu a ovládání snímacího a převodního zařízení (tzv. frame grabberu) obstarává program Grabpro, napsaný v programovacím jazyku C. V základní modulu Grabpro je vymezena posloupnost základních prováděných operac
í a komunikace s uživatelem; vlastní řídící a výpočetní operace jsou obsaženy v pomocných modulech. Moduly Commonip, Lutinit a Calcthresh slouží k řízení snímacího zařízení, nastavení zobrazovacích barev a určení prahu pro trasování obrysu z rozdělení jasů v obrazu. Moduly Czio a Grabsw slouží ke komunikaci s uživatelem. Vlastní určení obrysu kapky je obsaženo v modulu GrabTrac, jehož základem byl program převzatý z FEl ČVUT [l114] a některé podstatné procedury jsou upraveny z programu Račinského [l90]. Převod změřených parametrů Sk na parametry 1/H (oddíl i2.7.3) byl proveden v modulu RecH. Většina zbylých výpočtů je zavedena modulem Grabfce. Vlastní vyhodnocení je tedy obsaženo v modulech Grabfce a Grabtrac, které tvoří první přílohu. Přesnější výpočet je proveden z obrysů kapky a dalších parametrů měření, které jsou výstupem programu GrabPro. Určení parametru 1/H z obrysů kapek metodou několika vybraných rovin provádí program Vyhodsel, výpočet povrchového napětí z parametrů β a b nebo 1/H a de provádí program Pnzbeta. Oba programy jsou napsány v jazyku Turbo Pascal a tvoří i s jejich pomocnými moduly druhou přílohu. Z jimi použitých modulů Krivoper a KrivCtZap slouží ke čtení, zápisům a transformacím datových souborů, které mohou být v binárním či klasickém textovém formátu, popřípadě obsahovat data ve zhuštěném řetězovém kódu.Výpočet redukčních parametrů a povrchového napětí z PVT dat provádí program FitRedPar s pomocnými moduly Redparodhad (odhad redukčních parametrů pomocí objemové roztažnosti a isotermické stlačitelnosti dle oddílu i2.3.2.), Stavrov (provádí regresi parametrů stavových rovnic Newtonovou-Raphsonovou metodou), SimhyVy (vzájemně převádí redukovaný objem a
y v Simhově modelu na základě rovnice r2-54), Redprofil (provádí Cahnovu-Hilliardovu integraci rovnice (r2-66)). Program Pnzredparam počítá povrchové napětí ze zadaných redukčních parametrů, používá pomocné moduly Simhyvy a Redprofil. Tyto programy tvoří třetí přílohu. Výpočet mezifázového napětí a profilu je prováděn programem Mezifazi. Jeho modul Mezifdfn obsahuje definice typů užívaných jeho moduly, Mezifio komunikaci s uživatelem, Mezifsloz obsahuje procedury počítající složení fází, MezifQ zjišťuje q v aproximaci podle rovnice (r2-114) a MezifPost počítá profil rozhraní metodou postupného přiblížení. Výběr z těchto programů tvoří čtvrtou přílohu.Pro vyjádření výsledků měření některé veličiny (měrného tepla, hustoty, povrchového napětí) na některé z podmínek měření (teplotě, příp. čase, molární hmotnosti) se používají polynomy různého stupně. Pokud stupeň nevyplývá z teoretické rovnice pro vztah veličin, může být určen pomocí posouzení rozptylu experimentálních bodů od křivky. Podle literatury [l115, l116, l117] je pro regresi nejvhodnějším odhad
em rozptylu podíl residuálního součtu čtverců a počtu stupňů volnosti residuálního součtu čtverců, tj. rozdílu počtu experimentálních bodů a počtu parametrů v regresní rovnici. Tento rozptyl s rostoucím stupněm polynomu prochází minimem, jemuž příslušný polynom lze považovat za nejlepší přiblížení.Po konfrontaci s konkrétními výsledky byl volen jako nejvhodnější nejnižší ze stupňů, jimž odpovídající rozptyl není asi 1,5 až 2 krát větší než minimální rozptyl.
Rozptyl takto spočítaný plyne ze dvou zdrojů: z vlastního rozptylu měření při jednotlivých podmínkách a z proložení středních hodnot.
Druhou okolností, již je třeba vzít v úvahu, je nerovnoměrnost rozložení experimentálních bodů (např. při některých teplotách se podaří shromáždit více údajů). Nemá-li se těmto úsekům přikládat větší váha, lze rozdělit celou stupnici na oblasti podle hodnoty některé proměnné (např. u teplotních závislostí v této práci to byly zpravidla intervaly 2,5 K nebo 5 K, tj. asi 1/20 teplotního rozsahu), a pro výpočet použít body zí
skané zprůměrováním všech bodů v jednotlivých oblastech. Zároveň při lokálním průměrování lze získat odhad rozptylu vlastního měření a rozptyl zprůměrovaných bodů od křivky odráží lépe vlastnosti proložení s danými parametry, zejména se lépe identifikuje minimum rozptylu.