Na rozhraní mezi tekutými fázemi existuje mezifázová vrstva, ve které se mění vlastnosti směsi z hodnot odpovídajících jedné fázi na hodnoty fáze druhé [l1]. Tloušťka této vrstvy je obvykle řádu jednotek až desítek nm. Veličiny zde mají gradient kolmo k rozhraní, uvnitř fází jsou homogenní, odhlédneme-li od fluktuací. Hodnoty extensivních veličin v soustavě s fázovým rozhraním mohou být jiné, než je součet těchto veličin v odpovídajících
objemech uvnitř objemových fází. Poměry tohoto rozdílu k ploše fázového rozhraní se označují jako povrchové a mezifázové veličiny.K veličinám, jejichž změna v mezifázové oblasti je nejčastěji sledována, patří koncentrace složek (jim odpovídající povrchovou veličinou je povrchový přebytek), hustota a tlak (jemu odpovídá povrchové či mezifázové napětí).
Povrchové napětí je měřitelná síla, která existuje na všech kapalných površích; podobně na rozhraní kapalných fází existuje mezifázové napětí. Obě pramení z nesymetrického působení kohesních sil na molekuly v povrchové, popř. mezifázové vrstvě. Existence povrchového a mezifázového napětí se projevuje mimo jiné ve snaze kapalin tvořit kapky o minimálním povrchu a v jejich různém chování v kontaktu s další fází. Velikost povrchového napětí se pohybuje u běžných kapalin zpravidla v rozmezí desítek mN·m
-1 . Mezifázová napětí mezi polymery se pohybují zpravidla v jednotkách mN/m.K pojmu povrchového napětí lze dospět několika způsoby: popisně pomocí mechaniky spojitého prostředí, dále příčinně pomocí mechaniky na úrovni částic, a konečně pomocí makroskopické termodynamiky, kde se však vlastně jedná o volnou povrchovou energii, která je s povrchovým napětím svou velikostí i rozměrem shodná.
Odvození povr
chového napětí z pohledu mechaniky spojitého prostředí uvádí v precizní formě Goodrich [l2]:Tlak je obecně popsán symetrickým tensorem 2.řádu, tj. o 6 různých prvcích. V isotropním prostředí (objemová fáze) jsou si diagonální složky tlaku rovny a ostatní složky jsou nulové. O mezifází se předpokládá,že je válcově symetrické kolem osy kolmé na fázové rozhraní. Z podmínky invariance tenzoru tlaku vůči rotaci kolem osy symetrie plyne, že nediagonální složky budou nulové, diagonální složky
pT kolmé na osu symetrie si budou rovné a nezávislé na složce osové pN. Podmínkou mechanické rovnováhy je:∂pT /∂x = ∂pT /∂y = 0; ∂pN /∂z = 0 (R2-1)
kde x,y,z jsou kartézské souřadnice.
Složka
pN musí být v mezifázové vrstvě stejná jako v objemové fázi a je ztotožnitelná s hydrostatickým tlakem. Práce potřebná na deformaci takového systému popsanou tenzorem E o složkách eij je
W =Pr
otože v objemové fázi je tato práce
W = plze rovnici přepsat
W = pN V - A (R2-4)kde = ![]() (pN-pT) dz a A =
(pN-pT) dz a A = ![]() (exx+eyy)dx dy.
(exx+eyy)dx dy.
Veličina
se pak nazývá povrchové (mezifázové) napětí. V značí objem, A plochu.
Pro vyjádření závislosti povrchového napětí na hustotě se užívá McLeodova rovnice [l1]
=0n (R2-5)n v této rovni
ci při odvozování z teoretického modelu pole ostatních částic s Lennardovým-Jonesovým potenciálem vychází 8/3 [l3], pro polymery rovnice platí s hodnotou n 3 až 4,4, nejtypičtěji 4,0. Závislost povrchového napětí na hustotě poskytují i teorie, které jsou uvedeny v dalších kapitolách.
Pro běžné kapaliny se používá řada rovnic popisujících závislost povrchového napětí na teplotě. Tyto rovnice by měly respektovat skutečnost, že povrchové napětí je při kritické teplotě
Tc (mezifázové napětí při kritické teplotě odmíšení) nulové.Van der Waals navrhl rovnici
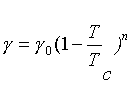 (R2-6)
(R2-6)
kde n = 1,23; rovnice se s hodnotou n = 11/9 nazývá též Guggenheimovou. Hodnota γ
0 se získá extrapolací povrchového napětí na nulovou teplotu.Teplotní součinitel povrchového napětí lze vyjádřit derivací Guggenheimovy rovnice (r2-6)
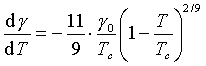 (R2-7)
(R2-7)
To znamená, že je-li např. kritická teplota látky 900 K, bude poměr teplotních součinitelů povrchového napětí při krajních 600 K a 300 K činit 2
2/9, tj. 1,17; závislost lze tedy čekat prakticky lineární.Pokud teplotní závislost povrchového napětí připíšeme toliko změně hustoty, získáme
d/dT=-n (R2-8)
kde n je exponent McLeodovy rovnice (r2-5),
teplotní objemová roztažnost. V rovnici povrchového napětí odvozené pomocí Lennardova-Jonesova potenciálu [l1] závisí na teplotě kromě hustoty ještě polární složka van der Waalsových sil, která s rostoucí teplotou slábne. To by mělo velikost teplotního součinitele o něco zvýšit.Teplotní součinitel povrchového napětí se obvykle pohybuje v desetinách mN·m-1·K-1, u polymerů kolem (0,05-0,10) mN·m-1·K-1. Teplotní součinitel mezifázového napětí polymerů se pohybuje kolem 10-2 mN·m-1·K-1.
Již dřívější autoři [l4] dospěli k závěru, že veličina [P]:
[P] = V1/4 (R2-9)
je aditivní (V je zde molární objem)
a lze její pomocí odhadovat povrchové napětí. Tato veličina byla nazvána parachor. Považujeme-li parachor za konstantu látky nezávislou na momentální hodnotě stavových veličin, je definiční rovnice parachoru konsistentní s McLeodovou rovnicí (r2-5).
Podobně jako některé objemové vlastnosti
q (skelná teplota, tepelná kapacita, teplotní objemová roztažnost, index lomu aj.) závisejí na molekulové hmotnosti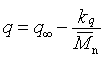 (R2-10)
(R2-10)
kde konstanta q
odpovídá veličině q extrapolované na nekonečnou molekulovou hmotnost, lze očekávat u povrchových vlastností závislost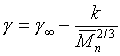 (R2-11)
(R2-11)
Vyjádřením hustoty pomocí molekulové hmotnosti [l1], jejím dosazením do McLeodovy rovnice s exponentem n, rozvojem v mocninnou řadu podle M a zanedbáním vyšších členů získáme
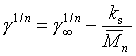 (R2-12)
(R2-12)
nebo
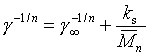 (R2-13)
(R2-13)
Tyto rovnice se užívají s hodnotou n = 4 a dávají někdy lepší výsledek než (r2-11) [l5], ale rozdíl v přesnosti není podstatný [l1]. Hodnoty γ
∞ v obou rovnicích jsou rozdílné. Závislost (r2-12) je však konzistentnější s experimentální závislostí g - T vysokomolekulárních látek i použitím parachoru.V oblasti vysokých molekulových hmotností však shledávají Dee a Sauer [l6] výstižnější lineární závislost
=-
K popisu vícesložkových nebo vícefázových soustav a předpovědi jejich vlastností se zavádějí modely. Některé modely používané na soustavy obsahující polymery uvádí následující oddíl. Jejich aplikace při teoretickém výpočtu povrchového napětí bude podána v oddíle d2.4.
Vztah mezi objemem, tlakem a teplotou látky se vyjadřuje stavovou rovnicí. Často je výhodné tyto stavové veličiny (Q) převést na jim přímo úměrné bezrozměrné redukované veličiny (
![]() = Q / Q* (R2-15)
= Q / Q* (R2-15)
Jako tyto parametry se volí takové v
eličiny týkající se dané látky, aby stejná redukovaná stavová rovnice platila pro různé látky.Patterson, Siow, Rastogi [l4, l7], Prigogine [l8] definují redukční parametry
V*(n) = NA r(n)(R*)3 (R2-16)
U*(n) = NA q(n
)(є*) (R2-17)S*(n) = NA c(n)k (R2-18)
T* = U*/S* = q(n
) є*/[c(n)k] (R2-19)p* = U*/V* = q(n) є*/r(n)(R*)3 (R2-20)
přičemž
n je počet atomů hlavního řetězce, r,q,c jsou různá možná vyjádření počtu segmentů v molekule; z nich se obvykle q ztotožňuje s r a označuje jako počet segmentů v molekule, 3c je počet vnějších stupňů volnosti molekuly, ε* je minimální energie mezi dvojicí segmentů (є*= z ε* mezi segmentem a okolνm) a R* jí odpovídající vzdálenost mezi segmenty. Čistý objem jednoho segmentu se značí v*= (R*)3/ λ, kde λ je geometrickύ faktor.Veličiny є
*, v* a c, r, popř.c/r, se označují jako mikroskopické redukční parametry; mají bezprostřední fyzikální význam související se strukturou látky. Veličiny p*,V*,T* jsou vyhodnotitelné z experimentálních PVT dat a spolu s U* a S* se nazývají makroskopickými redukčními parametry.Jestliže se počty segmentů
r a q ztotožňují, povrchové napětí může být redukováno parametrem [l6]* = (kp*2 T*c/r)1/3 (R2-21)
Způsob, kterým zavedli redukční parametry Sanchez a Lacombe [l9,l10], vztahuje mikroskopické redukční parametry k segmentu a nikoli k celé molekule. Do jejich redukčních parametrů se nepromítá rozdíl mezi počtem segmentů
r a počtem vnějších stupňů volnosti molekuly. Redukční parametry jsou definoványT
*= є*/k (R2-22)p*= є */v* (R2-23)
V*= NA rv* (R2-24)
redukční parametr є* představuje interakční energii segmentu v objemové fázi s ostatními segmenty soustavy. Součin
rv* je ztotožněn s objemem připadajícím na molekulu při nejtěsnějším uložení neuspořádané tekutiny. Bylo by jej možno ztotožnit i s objemy v krystalickém stavu, Sanchezovi a spol. [l9, l10] však dávala první varianta lepší souhlas s experimentálními daty.Redukovaná hustota je dána
![]()
Na rozdíl od redukčních parametrů v modelech Floryho, Prigogina [l8], Pattersona [l4, l7] atd. (buňkových modelech) jsou redukční parametry dle Sancheze a Lacombea navzájem vázány vztahem
p*v*=kT* (R2-26)
takže molární hmotnost segmentu je pomocí redukčního parametru objemu vztaženého na jednotku hmotnosti vyjádřena rovnicí
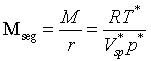
Redukční parametr povrchového napětí je zde
= (kp*2T*)1/3 (R2-28)
Redukční parametry se zpravidla vztahují ke konkrétní stavové rovnici, se kterou mají být užity. Určují se tedy tak, že k dané experimentální závislosti molárního nebo specifického objemu na teplotě a tlaku se hledají takové parametry
T*,p* a v*, aby vyhovovaly dané redukované stavové rovnici. Pro postup určení se uvádějí zejména dva postupy.Prvním z nich je klasická tříparame
trová nelineární regrese ze sady PVT dat [l11].Druhý postup, zavedený Florym (cit. dle [l7]), spočívá ve výpočtu z předem určených teplot, objemů, roztažností a stlačitelností. Je vhodný k použití při omezených PVT datech [l12], zejména pro atmosférický tlak a běžné teploty. Za těchto podmínek lze u většiny stavových rovnic pro polymery zanedbat člen, kde figuruje tlak, a stavovou rovnici lze pak přepsat do podoby
![]() (R2-29)
(R2-29)
Pro tepl
otní objemové roztažnosti α a isotermické stlačitelnosti β jsou redukčními parametry převrácené hodnoty redukčních parametrů teploty a tlaku:![]()
![]()
Proto jsou si rovny součiny ![]()
![]() = T.
= T.
Po zderivování stavové rovnice (r2-29) podle redukované teploty můžeme vyjádřit součin
T jako funkci redukovaného objemu:
T = F2 (Tím lze z teplotní závislosti objemu určit redukční parametr objemu. Redukční parametr teploty lze pak zjistit dosazením do stavové rovnice.
Redukovanou isotermickou stlačitelnost lze vyjádřit z redukovaných objemové roztažnosti, teploty a objemu, pro
Floryho model rovnicí [l7]:![]()
Je-li známa stlačitelnost, lze zjistit pomocí rovnic (r2-33) a (r2-31) i redukční parametr tlaku.
Často je používán Prigoginův [l8, l13] model kapaliny. Tento model je modelem buňkovým. Buňkové modely popisují soustavu rozdělenou na stejně veliké buňky. V každé buňce se nachází jeden segment, který se v ní může volně pohybovat. Celkový objem buňky je součtem vlastního objemu segmentu (v
yloučeného objemu) a volného objemu. Celková partiční funkce je proto dána součinem dvou funkcí.První z nich je konfigurační partiční funkce, zachycující stav, kdy jsou všechny segmenty uprostřed svých buněk. Tato funkce se řídí Lennard-Jonesovým potenciá
lem.Druhá z nich je buňková partiční funkce, týkající se vychylování jednotlivých segmentů z rovnovážné polohy uprostřed buňky. Pohyb v buňce se uvažuje dle modelu pravoúhlé potenciálové jámy s energiemi 0 uvnitř a ∞ mimo.
V následujících odstavcích bud
ou rovnice (7.3.3.) a další z Prigoginovy knihy [l8] vyjádřeny v redukovaných proměnných. Za redukční parametr teploty je bráno T*=z ε*/k , redukovaná Helmholtzova energie je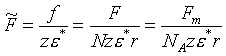 , přičemž f je Helmholtzova energie připadající na jeden segment, F celková Helmholtzova energie systému, Fm molární Helmholtzova energie. Podobně redukovaný chemický potenciál je
, přičemž f je Helmholtzova energie připadající na jeden segment, F celková Helmholtzova energie systému, Fm molární Helmholtzova energie. Podobně redukovaný chemický potenciál je 
Konfigurační Helmholtzova energie je
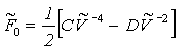 (R2-34)
(R2-34)
U rovnice pro pole nejbližších sousedů bylo C=1, D=2, při započítání dalších vrstev udávají autoři C=1,01, D=2,41. Pro oblast při povrchu by měly tyto konstanty klesnout, ale v níže uváděných teoriích se tímto způsobem k asymetrii silového pole nepřihlíží.
Buňková (volnoobjemová) Helmholtzova e
nergie je![]() (R2-35)
(R2-35)
kde ![]() je redukovaný volný objem, konstanta 2-1/6
je redukovaný volný objem, konstanta 2-1/6
Redukovaná Helmholtzova energie připadající na jednu buňku je
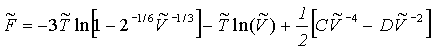 (R2-36)
(R2-36)
což lze zjednodušit na rovnici
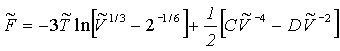 (R2-37)
(R2-37)
Vyjádřením tlaku jako derivace Helmholtzovy energie podle objemu p=-(∂
F/∂v)T vzniká stavová rovnice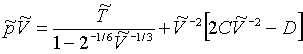
Při nízkém vnějším t
laku lze rovnici zjednodušit na![]()
Dee a spol. [l11 app.] používali pro vyhodnocení PVT dat též rovnici
![]()
![]()
která je záměnou za 2-1/6 0,89, B za C a A za D/2 totožná s(r2-38). Hodnotu používali 0,9532, A=1,2045, B=1,001
Rovnice (r2-37) nabývá v tomto zápisu tvaru
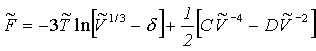
Floryho, Orwollův a Vrijův model [l14 podle l4, l7, l6, l8] se liší od Prigoginova modelu uvedeného v odst. i2.3.3 tím, že se potenciál mezi částicemi neřídí Lennard-Jonesovou rovnicí, ale je úměrný
r-3 a nemá složku odpovídající odpudivým silám. Proto je objem s minimální energií shodný s vyloučeným objemem. Redukovaný volný objem je (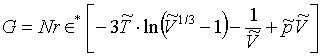 (R2-42)
(R2-42)
a stavová rovnice
![]()
která pro malé tlaky přechází v
![]() =
= ![]() -1(1-
-1(1-![]() -1/3) (R2-44)
-1/3) (R2-44)
Pro součin
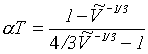 (R2-45)
(R2-45)
Sanchez a Lacombe [l9 ,l10] pracují s
redukčními parametry zavedenými jiným způsobem než u předchozích modelů, jak bylo uvedeno v oddíle i2.3.1. Zatímco u výše uvedených modelů Floryho a Prigogina se konektivita řetězce polymeru nepromítla do stavové rovnice, ale pouze do definice redukčního parametru teploty, Sanchez a kol. ji vzali v úvahu při odvození entropického členu. Volný objem není v modelu Sancheze a kol. na rozdíl od buňkového modelu vyjádřen volným objemem v buňkách, ale pouze existencí neobsazených míst v mřížce.Chemický potenci
ál je vyjádřen rovnicí
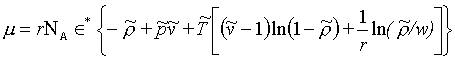 (R2-46)
(R2-46)
a stavová rovnice zpodmínky ![]() /v=~0:
/v=~0:
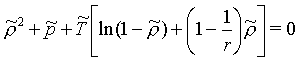 (R2-47)
(R2-47)
Redukční parametry určuje Sanchez z dat tense par (tlak nasycené páry), popřípadě z PVT dat podle rovnice (r2-47) nelineární metodou nejmenších čtverců. Parametr w v rovnici (r2-46) závisí na délce, ohebnosti a symetrii řetězce. Zpravidla jej není třeba znát, protože se pracuje s rozdíly potenciálů téže složky.
Výpočet všech redukčních parametrů jak podle rovnice (r2-33), tak určením parametrů rovnice (r2-47) vyžaduje data pro různé tlaky.
Pro případ omezených PVT dat navrhuje Sanchez [l12] odhad z experimentálních hodnot hustoty, objemové roztažnosti a stlačitelnosti určených za téže teploty a atmosfér
ického tlaku.Součin T α
je dán rovnicí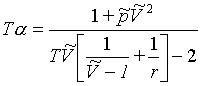 (R2-48)
(R2-48)
Simha a Somcynsky [l15] rozšířili buňkový model zmíněný v odstavci i2.3.3 tím, že uvažovali výskyt neobsazených buněk. Je-li jejich podíl y, platí pro Helmholtzovu energii připadající na jeden segment
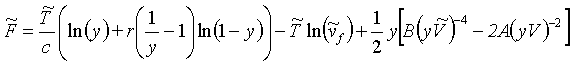 (R2-49)
(R2-49)
kde ![]()
![]() (R2-50)
(R2-50)
popřípadě přes segmenty:
![]()
Při ztotožnění počtů segmentů c a r nabývá rovnice (r2-49) tvaru
 (R2-52)
(R2-52)
První člen v rovnici (r2-52) má svou obdobu v Sanchezově rovnici (r2-46) pro Helmholtzovu energii. V Simhově modelu je však veličina y odlišena od redukované hustoty, takže při parciální derivaci redukované Helmholtzovy energie dle objemu, kterou se získává stavová rovnice, tento člen na rozdíl od Sanchezova modelu vymizí.
Pokud je v této práci dále uváděn Simhův model bez další specifikace, rozumí se jím varianta odpovídající rovnici (r2-50). V tomto případě má stavová r
ovnice tvar![]() (R2-53)
(R2-53)
Hodnotu y
lze určit zpodmínky minimální Helmholtzovy energie (f/y=0) derivací rovnice (r2-49).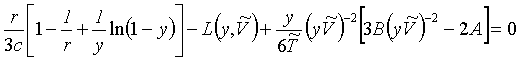 (R2-54)
(R2-54)
přičemž L je definováno
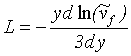 (R2-55)
(R2-55)
což při volném objemu dle rovnice (r2-50) poskytuje rovnici
L = 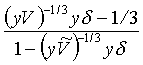 =
= 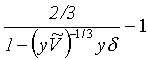 (R2-56)
(R2-56)
a podle varianty rovnice (r2-51)
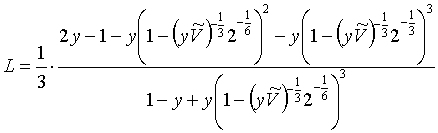
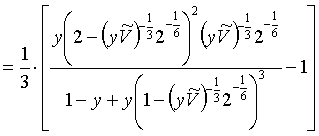 (R2-57)
(R2-57)
Dee a Walsh [l16] porovnávali jednotlivé stavové rovnice. Kritériem byl rozptyl experimentálních hodnot od nejlepšího proložení danou rovnicí v širokém rozsahu teplot a tlaků. Nejhorší výsledky poskytla rovnice (r2-47) ze Sanchezovy teorie, zhruba poloviční rozptyl Floryho rovnice (r2-43), o řád lepší byla Prigoginova rovnice (r2-38) a oproti ní mírně lepší Simhova a Somcynského rovnice (r2-53). V následující práci Dee a Walshe [l17] je jako ještě lepší ukázána rovnice (r2-40), kde je podstatným rozdílem
oproti rovnici (r2-38) adjustovatelnost parametru δ.
Cahn a Hilliard [l18] předkládají postup, jak vyjádřit u veličiny, jejíž závislost na složení v oblasti koncentračního gradientu umíme popsat, hodnotu jejího povrchového či mezifázového přebytku. Složení autoři vyjadřují molárním zlomkem jedné ze složek, který bude v následujících rovnicích podle citované práce [l18] označen
c. Složení může být vyjádřeno i jinou veličinou, kterou v dané soustavě můžeme jednoznačně popsat vyšetřovanou veličinu, např. hustotou, tlakem nebo koncentrací. Vyšetřovanou veličinou byla u Cahna a Hilliarda Helmholtzova energie F, pro určení povrchového napětí je příhodnější Gibbsova energie G, což na postupu nic nemění.Helmholtzova energie připadající na 1 molekulu (buňku) se vyjádří pomocí Taylorova rozvoje podle c a jeho gradientů (derivací podle prostorových souřadnic). Díky symetrii musí být některé členy rozvoje nulové. Celková energi
e systému o objemu V obsahujícího N molekul (rozděleného na N buněk) je vyjádřitelná rovnicí:F = ![]()
![]() [f0 + (c)2+... ]dV (R2-58)
[f0 + (c)2+... ]dV (R2-58)
kde f
0 je Helmholtzova energie na molekulu v homogenní fázi složení c a veličina κ je dána rovnicí
= -[2f/c2c]0 + [2f/ |c|2]0 (R2-59)Pro plochý povrch, kde existuje gradient koncentrace jen ve směru souřadnice x, vyjadřuje povrchovou energii rovnice
=kde
f(c) = f0(c)-[cB+(1-c)A] (R2-61)
i jsou potenciály složek v rovnovážných fázích.Pro rovnovážný koncentrační profil v povrchové vrstvě platí podmínka minimální Helmholtzovy energie, při jejímž splnění je
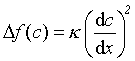 (R2-62)
(R2-62)
Za této podmínky lze rovnici (r2-60) transformovat do tvaru
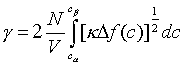 (R2-63)
(R2-63)
kde c
α a cβ jsou hodnoty c v objemových fázích.Známe-li funkci, která vyjadřuje hustotu Helmholtzovy energie (popř. energii na 1 částici) pomocí koncentrace, umožní rovnice (r2-63) výpočet povrchové energie.
Pro regulární roztok pak mohla být rovnice převedena do redukovaného tvaru
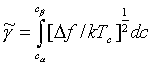 (R2-64)
(R2-64)
přičemž redukční parametr povrchového napětí je v tomto případě definován tak, že
γ =Tuto metodu použili pro polymery v mírně modifikované podobě Dee a Sauer [l6]. Jejich rovnice pro povrchové napětí je
![]() (R2-65)
(R2-65)
přičemž vztah k veličinám z rovnice (r2-63) je
 ,
, 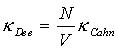 .
.
Index l označuje hodnotu v kapalné fázi, index v hodnotu pro páru. Odpovídající redukovaná rovnice má stejný tvar:
![]() (R2-66)
(R2-66)
Efektivní tloušťka povrchové vrstvy je definována
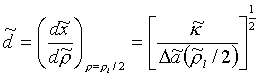 (R2-67)
(R2-67)
Skutečná efektivní tloušťka je pak
 (R2-68)
(R2-68)
Na rozdíl od Cahnovy a Hilliardovy rovnice (r2-64) není v rovnici (r2-66) κ zcela zahrnuto do redukθních parametrů, ale zůstává redukovaný parametr
Přijímá se předpoklad, že entropie nehomogenního systému závisí jen na místní hustotě a ne na jejím gradientu. Gradientový efekt je pak způsoben výlučně potenciální energií, pro niž pak
pak platí: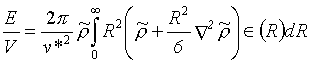 (R2-69)
(R2-69)
Nechť
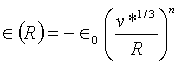 pro
pro 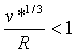 , (R)= ∞ pro menší R. Charakteristická interakční energie je
, (R)= ∞ pro menší R. Charakteristická interakční energie je
= 20/(n-3)a výsledek integrace rovnice (r2-69) je
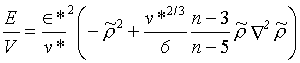 (R2-70)
(R2-70)
Pak
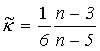 , pro n=6 je
, pro n=6 je Hodnota ![]() je určena
je určena
Pro a~ jsou pak zrovnic (r2-42) a (r2-46) odvozeny rovnice
kde
![]()
a pro Floryho model
![]() i = -3 ln (
i = -3 ln (![]() -1/3-1) (R2-74)
-1/3-1) (R2-74)
Veličina
![]()
Exponent je blízký hodnotě 4, která se vyskytuje v definici parachoru, proto byl vztah vyjádřen s tímto exponentem
![]()
Použitím redukčního parametru dle rovnice (r2-28) a porovnáním s rovnicí (r2-9) získal pro daný model vztah mezi redukčními parametry a parachorem:
[P]= [0,247kp*2T*]1/12V* (R2-77)
V modelu kapaliny podle Prigogina a Saragové [l21] platí pro redukované povrchové napětí
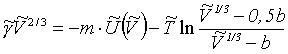 (R2-78)
(R2-78)
kde první člen na pravé straně plyne ze snížení počtu sousedních segmentů v povrchové vrstvě o m, druhý člen ze zvětšení partiční funkce při povrchu tím, že povrchové segmenty nejsou zvenčí omezovány v pohybu.
Výsledek dle rovnice (r2-78) shledávají Patterson a kol. [l7, l4] téměř shodný s rovnicí (r2-76), takže mohlo být povrchové napětí vyjádřeno
= 5,93510-9(J/K)1/3p*2/3T*1/3/Jimi rovněž uváděné starší vyjádření povrchového napětí pomocí rozpustnostního parametru přechází do tvaru
= 3,66110-9(J/K)1/3p*2/3T*1/3/(koeficienty u rovnic (r2-79) a (r2-80) jsou doplněny o rozměr a přepočítány na stejné jednotky s ostatními údaji v této práci). Výsledky obou rovnic jsou shodné pro redukovaný objem 1,29, který je běžnou hodnotou.
Fázovým rozhraním mezi polymery se zabývá několik teorií, uvedených v následujících oddílech.
V modelu řešícím povrchovou vrstvu rovnicí analogickou difusní rovnici vycházeli Helfand a Tagami [l22] z rovnice pro relativní partiční funkci q(
x,t). Rovnice vyjadřuje pro segmenty délky ls v potenciálovém poli U vliv interakcí a statistiky konformací v koncentračním gradientu na q a zní1/r [q(x,t)/t] = 1/6ls22q(x,t) - U(x)/kT q(x,t) (R2-81)
kde x
je poloha počátku řetězce a t zlomek jeho celkové délky r. Silové pole je tvořeno interakcí mezi segmenty a kohesními silami. Detaily jsou v [l22], v následujících odstavcích jsou uvedeny jen důležité vztahy plynoucí z modelu.Přibližné řešení koncentračního profilu ve fázovém rozhraní pro prakticky nestlačitelné systémy o velké délce řetězce je:
A(x)/0=2/(1+2) (R2-82)
B(x)/0=1/(1+2) (R2-83)kde = exp [(6)1/2x/ls] (R2-84)
a charakteristická tloušťka fázového rozhraní je
d = 0dx/dA (x=0) = 2ls/ (6)1/2 (R2-85)
Povrchové napětí je dáno:
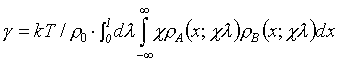 (R2-86)
(R2-86)
Při uplatnění profilů z rovnic (r2-82) až (r2-84) je pro povrchové napětí
= (/6)1/20lskT (R2-87)Pro profily získané bez této aproximace iterativním řešením je nutno povrchová napětí počítat numericky z vypočítaného profilu dle rovnice (r2-86).
Kromě uvedeného postupu pro symetrický systém (se složkami o stejně dlouhých segmentech a řetězcích) se Helfand a Sapse [l23] zabývali nesymetrickými systémy. Početní hustota segmentů složky k v čistém stavu je zde
Bk2=0klsk2/6 (R2-88)
a definován parametr ε pod
mínkou pro střední hustotu energie v soustavě (![]()
s kterým souvisí střed početních hustot segmentů v čistých složkách
![]()
Charakteristická tloušťka mezifází d byla definována rovnicí
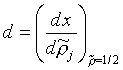 (R2-91)
(R2-91)
Řešením difusní rovnice s použitím přiblížení průměrného pole získali Helfand a Sapse pro tuto tloušťku výraz obdobný rovnici (r2-85)
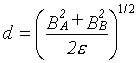 (R2-92)
(R2-92)
Pro mezifázové napětí získali vztah obdobný rovnici (r2-87)
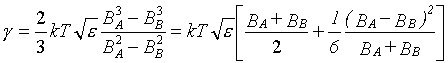 (R2-93)
(R2-93)
Eliminací ε z rovnic (r2-92) a (r2-93) plyne
AB~d-1.Redukovaná hustota zde použitá se liší od redukovaných hustot dle Floryho či Sancheze používaných v oddíle i2.3.3 tím, že v objemové fázi nabývají hodnoty 1. Svou podstatou jsou spíše bližší objemovému zlomku.
Jedním z často používaných východisek k popisu struktury a thermodynamických vlastností vícesložkových soustav je mřížkový model [l24]. Tento model předpokládá, že se jednotlivé složky skládají ze segmentů umístěných v uzlech mřížky, obdobné mřížce v krystalu. Někdy se místo pojmu uzel uží
vá též pojmů buňka či přihrádka. V teoriích, o nichž je níže referováno, je buňka obsazena právě jedním, popřípadě nejvýše jedním segmentem.V jednodušším přiblížení, kdy počítáme s interakčními energiemi pouze u sousedících segmentů, je směšovací teplo dá
no rovnicí
U = z(kde w
ij je energie kontaktu mezi částicemi i a j, z je počet sousedních míst v mřížce, Ni je počet segmentů složky i v soustavě, N celkový počet segmentů v soustavě. Pro zjednodušení výpočtů byl zaveden Flory-Hugginsův interakční parametr χ jako:
= z(kde k
je Boltzmannova konstanta.
V tomto modelu [l25, l26] je sous
tava tvořena nv vrstvami rovnoběžnými s povrchem. Vzájemná vzdálenost vrstev je b. Každá z nich obsahuje ns buněk o průřezu a. Každá buňka má z sousedů, z toho mz v každé ze sousedních vrstev a lz ve stejné vrstvě (2m + l = 1). V soustavě se nachází Nm molekul o rm segmentech (použitím postupu na polydispersní systém se zabývá odstavec i5.3.5.), a tedy počet segmentů každé složky m jenm= rmNm (R2-96)
příslušný objemový zlomek neboli podíl buněk mřížky obsazených danou složkou je pa
k (R2-97)
(R2-97)
Předpokládá se, že místní složení je vždy v celé vrstvě stejné bez ohledu na to, jakou polohu v řetězci zaujímají zde se nacházející segmenty. Objemový zlomek složky m ve vrstvě i se označuje
Efektivní tloušťka fázového rozhraní je definována
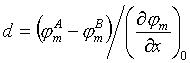 (R2-98)
(R2-98)
kde značka veličiny s indexem A nebo B označuje její hodnotu v příslušné objemové fázi. Jmenovatel představuje derivaci v místě, kde je
Příspěvek jednoho segmentu umístěného ve vrstvě i k Helmholtzově energii systému je dán rovni
cí (lokální formulace Floryho-Hugginsovy rovnice):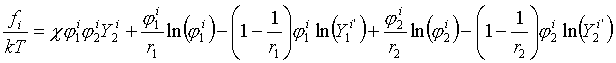 (R2-99)
(R2-99)
kde
![]() (R2-100)
(R2-100)
![]() (R2-101)
(R2-101)
kde ![]()
Zprůměrování těchto hodnot nejen v rámci jedné vrstvy, ale v celé oblasti rozhraní, je asi jedním z prvních předpokladů, které by bylo při zpřesňování třeba opouštět.
O rovnovážném koncentračním profilu se předpokládá, že je dán hodnotami
je tedy profil určen rovnicí
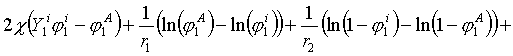
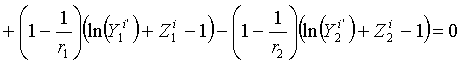 (R2-102)
(R2-102)
kde
Zmi= m/Ymi+1' + m/Ymi-1' + l/Ymi' (R2-103)
V dalším postupu pak byl rozdíl mezi Y'a Y zanedbán.
Mezifázové napětí je dáno jako rozdíl vztažený na jednotku plochy mezi skutečnou Helmholtzovou energií systému, která je dána součtem volných energií jednotlivých vrstev, a Helmholtzovou energií hypotetického systému bez mezifázové vrstvy. Helmholtzova energie
F0 zmíněného hypotetického systému je vyjádřena pomocí chemických potenciálů složek a množství v objemových fázích rovnicíF0= 1N1 + 2N2 (R2-104)
a
a Helmholtzovu energii celého systému pak vyjadřuje rovniceF = A + 1(N1+A1) + 2(N2+A2) (R2-105)
Kombinací rovnic (r2-99) a (r2-104) vzniká
![]() (R2-106)
(R2-106)
Roe uvádí několik řešení pro symetrický systém s nekonečnými řetězci. Pro případ χ podstatně většího než kritická hodnota (χ
- χc>2 pro přesnost několika procent) předpokládá jen 2 přechodové vrstvy s objemovými zlomky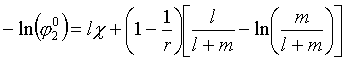
Pro mezifázové napětí pak je:
a/kT m - 2 (1-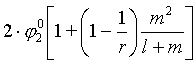 (R2-108)
(R2-108)
V případě
blízkému kritické hodnotě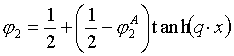 (R2-109)
(R2-109)
kde x
je délková souřadnice kolmo k fázovému rozhraní, q konstanta. Jak patrno z rovnice (r2-109), je charakteristická tloušťka přechodu d = 2/q.Pro podmínku (c « c2 ), tj. pro nejbližší okolí kritického bodu, pak uvádí Roe vztahy
a/kT (m/2)(-c)3/2r (R2-110)q = (r/2bm1/2)(-c)1/2 (R2-111)
Rovnice ukazují, že s rostoucí délkou řetězce mezifázové napětí roste a tloušťka mezifázové vrstvy klesá.
V limitě pro nekonečně dlouhé řetězce získal Roe [l25] pro mezifázové napětí polymerů o stejně dlouhých řetězcích výrazy, které se zanedbáním některých členů zjednodušily na
a/kT a
q 2-3/4m-1/21/4.b-1 (R2-113)
Jako dobrá aproximace pro nesymetri
cký systém se jevila zobecněná rovnice (r2-109): ![]() (R2-114)
(R2-114)
Helfand [l27] upozorňuje, že postup při výpočtu partiční funkce ve zmíněné Roeově práci bere v úvahu počet možných stavů bez ohledu na nestejnou pravděpodobnost jejich uskutečnění; byl by zcela platný pouze při stejné pravděpodobnosti realizace uvažovaných mikrostavů, což v mezifázové oblasti není splněno.
Z rovnice (r2-108) získáváme pro závislost mezifázového napětí na molekulové hmotnosti pro dvojici polymerů o stejně dlouhých řetězcích rovnici (r2-14).
Helfand [l27] při použití mřížkového modelu přihlížel k anisotropii pravděpodobností vazeb vycházejících ze segmentů: zatímco u Roeova modelu byla pravděpodobnost vazby z vrstvy i do vrstvy i+1 odvozována z počtu míst a složení vrstvy:
gik+![]() = g-i+1,k
= g-i+1,k![]() (R2-115)
(R2-115)
Při zavedení proměnných
ik = -ln (gik0) (R2-116)
ik = - ik - ln (gik+) i-1,k = + ik + ln (gik-) (R2-117)![]()
je pak koncentrační profil dán soustavou rovnic
![]() (R2-119)
(R2-119)
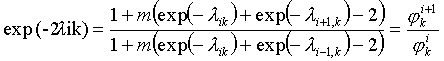 (R2-120)
(R2-120)
a
pro mezifázové napětí je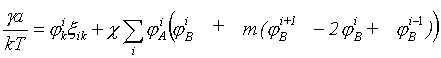 (R2-121)
(R2-121)
V quasispojitém případě přechází (r2-120) na
ik= -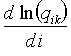 -
- 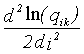 (R2-122)
(R2-122)
kde q je zavedeno
qik2= ![]() (R2-123)
(R2-123)
a ik je
ik=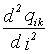 (R2-124)
(R2-124)
Zrovnice (r2-118) tím vznikne 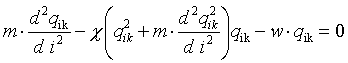 (R2-125)
(R2-125)
To odpovídá rovnici difusního modelu zmiňované v [l22], zatímco o Roeově řešení pro mřížkový model Helfand uvádí, že neposkytne pro quasispojitý případ rovnici totožnou s rovnicí z modelu náhodné procházky a s rovnicí (r2-125).
Při zanedbání členu s druhou derivací (tzv. efektu nelokální energie) je rovnice profilu
![]() (R2-126)
(R2-126)
a pro mezifázové napětí a charakteristickou tloušťku platí:
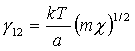 (R2-127)
(R2-127)
a
d =2(m/)1/2 (R2-128)
Bez zanedbání tohoto členu získal Helfand rovnici profil
u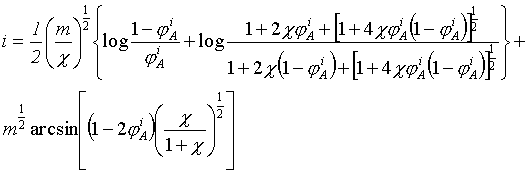 (R2-129)
(R2-129)
kde i je index vrstvy,
kde i je index vrstvy,
a rovnici pro mezifázové napětí
12=
Helfandův difusní model:
Použití spojitého modelu je na místě, nejsou-li koncentrační gradienty příliš velké, což u nekompatibilních polymerů nebude dobře splněno. Přihlíží k hustotním fluktuacím prostřednictvím stlačitelnosti.
Roeův mřížkový model:
Vyloučení dvojího obsazení buňky a ohebnost řetězce se projevuje prostřednictvím rozdílné hodnoty
lz v entropickém a entalpickém členu, která se při praktickém výpočtu nebere v úvahu. Naproti tomu je model použitelný i pro polymery s řetězci konečné délky (i pro systém polymer - monomer); předpokládá objemové fáze ne čisté, ale vzájemně nasycené (dle Floryho-Hugginsovy rovnice).Helfandův mřížkový model:
Zde uvedená prezentace dle [l27] počítá s molekulami prakticky nekonečně dlouhými, s čistými objemovými fázemi. Odlišnost od volně spojeného řetězce a případné vyloučení dvojího obsazení je explicitně vyjádřena faktory
gik. V spojité limitě řešení splývá s difusním modelem.