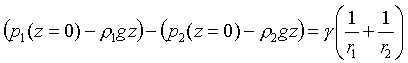 (R2-132)
(R2-132)Přehledy metod měření povrchového napětí uvádí např. Wu [l1] a Padday [l3]. První skupina metod je založena na měření síly, další skupina vychází z tvaru povrchu, který je výslednicí silového působení. Polymery se zpravidla vyznačují vysokou viskozitou, která často ovlivní naměřené síly výrazněji než povrchové napětí. Proto jsou vhodné k jejich měření metody z druhé jmenované skupiny. Za nejvhodnější k měření povrchového i mezifázové
ho napětí polymerů je zpravidla považována metoda visící kapky.Profilové metody (visící, sedící a rotující kapka) využívají skutečnosti, že tvar kapky je výslednicí působení povrchového napětí a gravitační, u rotující kapky odstředivé síly. Pro výpočet povrchového napětí je nutno znát hustotu. Výhodami metody je, že při měření není povrch ovlivňován materiály použitými při konstrukci měřicího přístroje, že se měřením nemění velikost povrchu a že měření probíhá v relativně snadno dosažitelné mechanické rov
nováze. Z těchto metod je nejrychlejší metoda visící kapky; její možná potíž spočívá v případném předčasném odtržení kapky.Všem metodám je společný požadavek vyloučení vibrací při měření; zvláště citlivé jsou metody profilové.
Pro určování povrchového a mezifázového napětí polymerů jsou nejvhodnější metody, které vycházejí z tvaru rozhraní. Teoreticky vycházejí z rovnice pro válcově symetrické povrchy v homogenním tíhovém poli [l3, l65, l2, l67, l66]. Na zakřiveném rozhraní je na vnitřní straně povrchu přetlak
p = (c1+c2) = 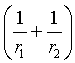 (R2-131)
(R2-131)
kde c
i jsou jeho hlavní křivosti (ri poloměry křivosti).V homogenním tíhovém poli o zrychlení g
pak rovnice pro zakřivení rozhraní mezi prostředími o hustotách ρ1 a ρ2 v bodě daném souřadnicí z ve směru osy symetrie přechází na: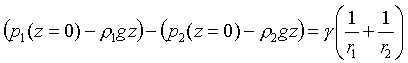 (R2-132)
(R2-132)
což nabývá vyjádřením rozdílu veličin
q: Δq = q2- q1 podoby-p(z=0) + gz = 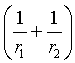 (R2-133)
(R2-133)
kde Δ
p je rozdíl tlaků v místě nulové souřadnice z, která se umisťuje do průsečíku osy symetrie s tečnou rovinou plochy fázového rozhraní kolmou na tuto osu, r1 a r2 jsou poloměry křivosti orientované na stranu fáze 1.V případě kapek, bublin, menisků v kapiláře apod.
je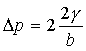 , přičemž b je poloměr křivosti ve vrcholu kapky (menisku), z=0 odpovídá vrcholu kapky.
, přičemž b je poloměr křivosti ve vrcholu kapky (menisku), z=0 odpovídá vrcholu kapky.
V tomto případě přechází rovnice (r2-133) do tvaru
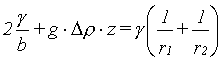 (R2-134)
(R2-134)
Člen na pravé straně lze přepsat jako
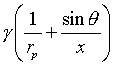
kde rp
je poloměr křivosti meridianové křivky kapky (což je křivka, kterou vidíme na obrázku o1), θ je úhel normály povrchu kapky s osou symetrie, přičemž x je souřadnice kolmá k ose symetrie.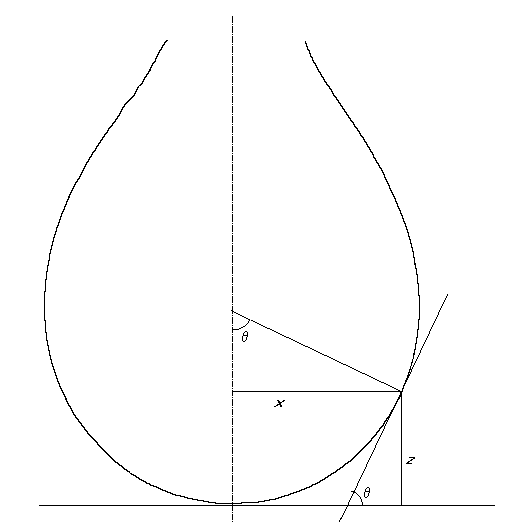
Obrázek O1:
Visící kapka a její zakřiveníZavedeme-li bezrozměrné proměnné tvaru Z =
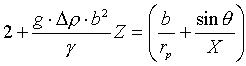 (R2-135)
(R2-135)
Fyzikální veličiny vystupují v jediném parametru, značeném
obvykle
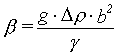 (R2-136)
(R2-136)
(např.J.F.Padday [l3] na str. 83 ). Takto definovaná hodnota je pro visící kapku záporná, pro sedící kladná. Často se také symbolem β značí hodnota opačného znaménka (např.Ambwani [l67]).
Pro výpočty je nejvýhodnější použít rovnice ve tvaru [l68,l
69] (2+Z)=![]() +
+![]() (R2-137)
(R2-137)
kde cos=dSdX sin=dSdZ
a S je oblouk od vrcholu kapky.
Někteří autoři [l70] užívají pro převedení rovnice (r2-134) do bezrozměrného tvaru parametru C =
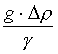 ; parametry jsou pak definovány X = x √C , Z = z√C , B = b√C (což je β ) a rovnici (r2-137) odpovídá
; parametry jsou pak definovány X = x √C , Z = z√C , B = b√C (což je β ) a rovnici (r2-137) odpovídá
(2/B+Z)=![]() +
+![]() (R2-138)
(R2-138)
Při kontrolním výpočtu pro β = 0 (kružnice) s krokem S 0,0001 dávala rovnice (r2-137) výsledky přesnosti asi 0,000001.
Měřit zakřivení ve vrcholu kapky by činilo potíže, proto se pro metodu visící kapky definuje výhodnější parametr
H vztahem [l71, l3]H=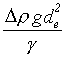 (R2-139)
(R2-139)
kde de je
maximální průměr kapky. Mezi H a je vztah: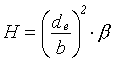
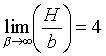 (R2-140)
(R2-140)
Pro měření povrchového napětí se zjišťují vhodné rozměry kapky, které jsou voleny tak, aby byly vzájemně jednoznačnou funkcí parametru β. Tuto podmínku splňují například poměry průměru kapky dk v rovinách, vzdálených od vrcholu o k-násobek maximálního průměru, k tomuto maximálnímu průměru de (metoda vybrané roviny), značené Sk= dk/de. Základní hodnota k je 1, pro kterou se hodnota průměru d1.0 označuje dS, rozsah používaných k je od 0,8 do 1,2. Odečítání de a ds znázorňuje obrázek o2.
Pro vyhodnocení povrchového napětí se pomocí tabulek
H - Sk určí H (v praxi zpravidla 1/H) odpovídající naměřeným poměrům Sk. Z něj se vypočítá povrchové napětí. Jak patrno ze vzorce, je k výpočtu zapotřebí i znalosti hustoty vzorků. Jsou-li hodnoty H určené z různých rovin stejné, je to známka mechanické rovnovážnosti kapky [l28, l72, l73].Zmíněné tabulky se získávají výpočtem křivek odpovídajících jednotlivým hodnotám parametru β
.Fordhamovy [l74] a Staufferovy [l75] tabulky 1/H S1.0
uvádí např. Padday [l3] a Ambwani [l67], ukázku pro S1.2 Roe [l72]. Pro k 0,8 až 1,2 byly počítány vlastní tabulky. Podle Roea [l72] je ke zpracování tvarů visících kapek určených s běžným rozlišením zapotřebí přesnosti tabulek na 4.desetinné místo.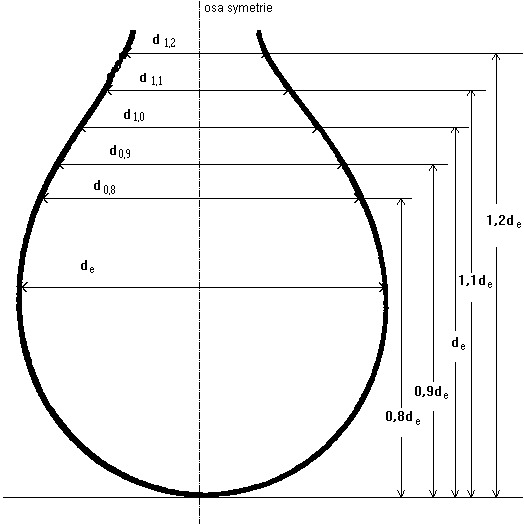
Obrázek O2: Odečítání parametrů visící kapky
Výsledky integrace lze pro snadnější zpracování zejména výpočetní technikou s určitou nepřesností nahradit rovnicemi aproximujícími závislost
H na S. Jednodušší z nich jsou typu1/H=keS-k , (R2-141)
přesnější mají tvar
1/H=k
eS-km+k3S3+k2S2+k1S+k0 (R2-142)Rovnici (r2-142) prezentoval Misak [l76]; jeho koeficienty pro tuto rovnici jsou uvedeny v tabulce t2.15.
Tabulka T2.15: koeficienty Misakových rovnic
|
interval S |
k 0 |
k 1 |
k 2 |
k 3 |
k e |
k m |
||
|
od |
do |
|||||||
|
0,9 |
-0,20970 |
-0,18341 |
1,08315 |
-0,69116 |
0,30715 |
2,84636 |
||
|
0,9 |
0,68 |
-0,05877 |
0,14701 |
-0,09155 |
0 |
0,31345 |
2,64267 |
|
|
0,68 |
0,59 |
-0,05285 |
0,15756 |
-0,11714 |
0 |
0,31522 |
2,62435 |
|
|
0,59 |
0,46 |
-0,13261 |
0,50095 |
-0,46898 |
0 |
0,31968 |
2,59725 |
|
|
0,46 |
0,40 |
-0,18069 |
0,84059 |
-0,97553 |
0 |
0,32720 |
2,56651 |
|
Při vyhodnocování se nejčastěji určuje jen poměr S1.0 pro vybranou rovinu vzdálenou od vrcholu kapky o hodnotu jejího maximálního průměru (Eley [l77], Nakajima [l78], Badran [l79], Patterson a Ross [l80], Rastogi [l81 l82], Zemanová [l83] aj. Odečtu ve více rovinách používali např. Roe [l72] a Wu [l28] pro 0,8 až 1,2 násobek maximálního průměru, pro výpočet povrchového napětí průměrovali 1/H. Roeova postupu i jeho tabulek využíval Nakajima [l78]. S násobky 0,75 až 1,5 pracovali Ramakrishnan et al. [l73].
O
dolnější proti chybám jsou výpočty, které přímo nastavují parametry rovnic (r2-135, r2-137, r2-138) tak, aby s nimi zmíněné rovnice co nejlépe odpovídaly průběhu zjištěného profilu. Jeden z postupů pro výpočet vyvinul Rotenberg [l69]. Při jeho postupu se variují parametry a b teoretické křivky na minimální odchylku od křivky experimentální z výchozích hodnot β - 0,5 a b zjištěného přibližně ze zakřivení v počátku. Počet bodů užívaných pro tento postup je 20-60, nejvhodnějším z hlediska kompromisu rychlosti s přesností je 30-40 bodů. Značnou výhodou metody je, že není nutná lokalizace vrcholu křivky, jež je při klasickém postupu jedním ze zdrojů nepřesnosti. Rotenbergova výpočetního postupu používá i Chiwetelu [l84], zpracovávající průměry 30 párů hodnot obou větví křivky; výsledek kontroluje S - H tabulkami. Anastasiadis [l85] prováděl pětiparametrovou optimalizaci - 3 parametry na nastavení polohy obrazu (rotační úhel a x a y translace), dále zvětšení a tvarový faktor. Počátek souřadnic pro jeho postup může být umístěn ve vrcholu kapky nebo v jejím středu; u vyhlazených křivek jsou obě volby ekvivalentní, u nehlazených dává lepší výsledky střed. Ve srovnání s Rotenbergovým postupem dává stejné výsledky tam, kde Rotenbergův postup konverguje k fyzikálně reálným řešením. Anastasiadův algoritmus je odolnější vůči šumu, Rotenbergův postup zase nevyžaduje referenční bod. Výpočetní postup s minimalizací odchylky parametrů a b používá i Huh [l86] s použitím 35-55 bodů.Použití objemu pod určitou rovinou pro výpočet je méně obvyklé. Postupoval takto např. Girault [l87], který doporučuje tuto metodu pro případ napojení experimentu na výpočetní techniku, protože při této metodě odpadají chyby z numerického derivování a není třeba užívat tabulek.
Při ručním zpracování nepředstavuje určení obrysu při dostatečném kontrastu problém.
Při samočinném hledání obrysu hraje zpravidla základní roli prahová hodnota jasu. Ta je v jednodušším případě nastavována ručně tak, aby s jejím použitím získaný obrys odpovídal experimentátorově představě. Početně může být pro práh použit průměr mezi vrcholky histogramu četnosti jasů (Girault [l88]) nebo minimum mezi vrcholky histogramu (Anastasiadis [l85]). V případě naší aparatury bývá i několik minim
četností jasu s nulovou hodnotou, průměr mezi nejvíce zastoupenými jasy leží v oblasti výskytu těchto minim.Obrys samotný se určí hledáním, kde spolu sousedí body s jasem nad prahem a pod prahem. Hledání je možno provádět systematicky po vodorovných či svislých přímkách, nebo podél obrysu od jeho prvního určeného bodu [l89]. Není-li osvětlení dost rovnoměrné, umožní detekci použití lokálního prahu či hledání maximálního gradientu. Názory na přínos těchto metod k přesnosti za dobrého osvětlení se různí (
[l85,l90,l91]). Pro případ, kdy tomu nebrání žádaná rychlost měření, se zdá rozumnější těchto metod k zpřesnění využít. Račinský [l90] a Hansen [l91] nacházejí 2 body mající intenzitu nad a pod prahem a určují přesnou polohu lineární interpolací. Neinterpolují však ve směru kolmém na hranu, ale Račinský pouze horizontálně pro oblast mimo vrchol kapky, Hansen podle směru hrany na vertikále nebo horizontále. Tato metoda je citlivá k šumu, protože používá jen dva body, použití více bodů však prodlouží čas, aniž by se výsledek zpřesnil výrazným způsobem.Zjištěný profil se může zpřesnit vyhlazením polynomem 3. nebo 4. stupně. Anastasiadis [l85] při této operaci otáčel dané skupiny bodů podle jejich sklonu, a po spočítání se středový bod transformoval zpět do původních souřadnic.
visící kapky a příbuznými metodami
S2.7.5.1. Uspořádání aparatur
Zařízení k měření uvedenými metodami se skládají téměř vždy ze zdroje světla, prostoru se vzorkem a snímacího zařízení (fotoaparátu, mikroskopu nebo kamery).
S2.7.5.2. Získání a záznam obrazu
Hlavními problémy jsou dostatečná ostrost a kontrast obrysů a nezkreslení rozměrů kapky, které jsou ovlivněny osvětlením kapky a snímací optikou, a vibrace, které jednak rozostřují obraz, jednak uvádějí kapku do nerovnovážného stavu, pro který rovnice (r2-132) a tím i z ní odvozené rovnice neplatí, protože působí kromě povrchové a gravitační síly i setrvačnost pohybující se kapaliny a její vnitřní tření.
Kapka bývá zp
ravidla osvětlována zezadu; někteří autoři [l68,l28,l31] používají nebo doporučují monochromatické světlo, názor na jeho potřebnost však není jednotný. Není-li rozdíl indexů lomu obou látek dostačující, může kontrast zlepšit změna osvětlení. Nguyen [l92] navrhuje vnitřní osvětlení kapky, kterého se dosáhne montáží např. malého diaprojektoru nad trubičku, ze které je kapka vypouštěna. Oproti osvětlení zezadu tato metoda poskytuje ostřejší obraz, ale za cenu řádově delší expozice. Autorem uváděná větší jednoduchost takového zařízení oproti osvětlení zezadu je sice sporná, nicméně tento způsob osvětlení umožňuje zaznamenání obrazu u některých dvojic kapalin, kde by to při osvětlení zezadu nebylo možné bez barvení nebo jiné úpravy, ovlivňující měřenou veličinu.Ostrost obrazu kapky sice zvýší použití blesku, ale nezaručí její rovnovážnou polohu, proto se nedoporučuje [l31]. Protože je zapotřebí ostrého a nezkresleného obrazu s pokud možno rovnoměrným osvětlením, používá se světlo rozptýlené [l93, l94] nebo para
lelní [l31, l95, l82, l96], někdy i polarizované [l93].Jako zobrazovací soustavy se užívá někdy jediného objektivu s ohniskovou vzdáleností kolem 100 mm (Girault[l87,l88], Nakajima [l78], Matsubara [l94]). Výhodou je méně zkreslujících činitelů v optické soustavě, nevýhodou především značná délka optiky v uspořádání, kdy má být dodržena určitá vzdálenost optiky od kapky při zajištění dostatečného zvětšení. Zřejmě častější je užívání mikroskopů, dvojice objektivů či teleobjektivů (Patterson, Ross [l80], Ba
mberger [l97], Boyce et al. [l93], Chiwetelu [l84], Rastogi [l81 l82], Bhatia [l32], Kakiuchi [l68], Roe [l31], Smith [l98], Wu [l28]).Kvůli konstantnímu zvětšení je zapotřebí zaostřovat posunováním měřicího bloku, tj. beze změny vzájemné polohy optických prvků [l28,l31,l82,l98].
Obraz je možno kalibrovat více způsoby. Například Ambwani [l67] uvádí:
1. Mikrometrický disk se stupnicí, umístěný na místo kapky (podle [l82])
2. Ocelová kulička přesně známého průměru (umístěná na místo kapky) nebo jiné těles
o [l88], Ramakrishnan et al. [l73]3. Visící kapka o známém povrchovém napětí
Obvyklé je určování rozměrů pomocí změřené kapiláry, z níž je kapka vypouštěna [l93, l94, l95].
S2.7.5.3. Vyloučení vibrací
Jak se ukázalo i při této práci, rušení způsobené vibracemi může být značné. Řada autorů uvádí, jak řešili tento problém. Např. Patterson a Ross [l80] a Andreas [l71] měli aparaturu na masívním bloku (1 t) na pneumatikách. Kakiuchi [l68] užíval gumovou podložku. Pro vyloučení otřesů bývá kamera, která by mohla být jejich příčinou, často umístěna mimo odpružený stůl [l79, l80]. Roe [l31] měl celé zařízení kvůli vibracím na bytelné železné konstrukci v přízemní laboratoři.
S2.7.5.4. Pracovní komora
Pro měření za vyšších teplot většina autorů používá hliníkový blok s regulací teploty topnou spirálou (Wu [l28, l29], Roe [l72], Kakiuchi [l68]), méně obvyklá je olejová lázeň (Rastogi [l82]). Přesnost regulace teploty bývá uváděna až 0,01%C.
Kapilára, z které je vypouštěna kapalina, je zpravidla z nerez oceli (Andreas [l71], Bhatia [l32], Chiwetelu [l84], Nakajima [l78], Boyce [l93], Ramakrishnan [l73]), někdy skleněná (pyrex sklo Wu [l28], Hata [l99], Jennings [l100], Anastasiadis [l101]). Volbu materiálu ovlivňují kapilární jevy.
Při měření tavenin polymerů je užívána dusíková [l31] nebo argonová [l28, l29] atmosféra.
Z četných metod měření hustoty kapalin jsou vzhledem k vlastnostem polymerů a požadované přesnosti použitelné jen některé.
Jsou to metoda pyknometrická, dilatometrické met
ody, metody založené na rovnici harmonických kmitů, vztlakové metody.Přesnost pyknometrické metody bývá uváděna 10
-3 g·cm-3. Metoda spočívá ve vážení vzorku v nádobce známé hmotnosti a objemu. V souvislosti s měřením povrchového napětí ji používali např. LeGrand, Bender, Gaines [l42, l48].Dilatometrická metoda v uspořádání popsaném Bekkedahlem [l102] umožňuje přesnost měření 3 10
-6g·cm-3 [l103]. Hustota se měří nepřímo pomocí objemu známé pracovní kapaliny, která musí být v celém teplotním rozsahu měření kapalná a netěkavá, známé teplotní roztažnosti, inertní vůči vzorku, dostatečně tekutá. Klasickou pracovní kapalinou je rtuť. Metoda je často používána zejména ve starších precizních pracích k určení hustoty jako údaje při měření povrchového napětí (Wu [l28, l29, l30], Roe [l31, l52], Bender [l48] , Rastogi [l82], Zemanová [l83]).Přesnost metody měření magnetickým plovákem se uvádí 2 10
-8g cm-3. Spočívá v měření nadlehčení tělesa přesně známého objemu při vážení v měřené kapalině. Omezuje ji viskozita kapaliny. Užití pro měření povrchového napětí uvádí Boyce et al. [l93].Další metoda využívá závislosti vlastní frekvence
ω kmitající soustavy na její hmotnosti m: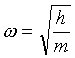 . Přístroj měří čas, za který kmitající kapilára vykoná určitý počet kmitů. Je zapotřebí kalibrace kapalinou známé hustoty, způsob je zvláště výhodný pro určování rozdílů hustot. Přesnost metody se uvádí 10-6g cm-3. V souvislosti s měřením povrchového napětí se používá spíše na nízkomolekulární látky, kde je velmi oblíbený (např. [l84]). Na tomto principu jsou založeny komerční densimetry firmy Anton Paar. Tyto přístroje zatím existují v provedeních do 140°C, na našem pracovišti však pouze do 60°C, proto nemohly být pro měření tavenin polymerů použity.
. Přístroj měří čas, za který kmitající kapilára vykoná určitý počet kmitů. Je zapotřebí kalibrace kapalinou známé hustoty, způsob je zvláště výhodný pro určování rozdílů hustot. Přesnost metody se uvádí 10-6g cm-3. V souvislosti s měřením povrchového napětí se používá spíše na nízkomolekulární látky, kde je velmi oblíbený (např. [l84]). Na tomto principu jsou založeny komerční densimetry firmy Anton Paar. Tyto přístroje zatím existují v provedeních do 140°C, na našem pracovišti však pouze do 60°C, proto nemohly být pro měření tavenin polymerů použity.